题目内容
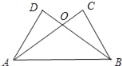
【题目】如图,在矩形纸片ABCD中,AB=6,BC=8.把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G;E、F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE沿EF折叠,使点D落在D′处,点D′恰好与点A重合.

(1)求证:△ABG≌△C′DG;
(2)求tan∠ABG的值;
(3)求EF的长.
【答案】(1)根据翻折变换的性质可知∠C=∠BAG=90°,C′D=AB=CD,∠AGB=∠DGC′,故可得出结论;(2)![]() ;(3)
;(3)![]()
【解析】试题分析:(1)根据翻折变换的性质可知∠C=∠BAG=90°,C′D=AB=CD,∠AGB=∠DGC′,故可得出结论;
(2)由(1)可知GD=GB,故AG+GB=AD,设AG=x,则GB=8-x,在Rt△ABG中利用勾股定理即可求出AG的长,进而得出tan∠ABG的值;
(3)由△AEF是△DEF翻折而成可知EF垂直平分AD,故HD=![]() AD=4,再根据tan∠ABG即可得出EH的长,同理可得HF是△ABD的中位线,故可得出HF的长,由EF=EH+HF即可得出结论.
AD=4,再根据tan∠ABG即可得出EH的长,同理可得HF是△ABD的中位线,故可得出HF的长,由EF=EH+HF即可得出结论.
试题解析:(1)∵△BDC′由△BDC翻折而成,
∴∠C=∠BAG=90°,C′D=AB=CD,∠AGB=∠DGC′,
∴∠ABG=∠ADE,
在△ABG与△C′DG中,
∵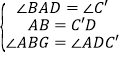 ,
,
∴△ABG≌△C′DG(AAS);
(2)∵由(1)可知△ABG≌△C′DG,
∴GD=GB,
∴AG+GB=AD,
设AG=x,则GB=8-x,
在Rt△ABG中,
∵AB2+AG2=BG2,
即62+x2=(8-x)2,
解得x=![]() ,
,
∴tan∠ABG=![]() ;
;
(3)∵△AEF是△DEF翻折而成,
∴EF垂直平分AD,
∴HD=![]() AD=4,
AD=4,
∴tan∠ABG=tan∠ADE=![]() ,
,
∴EH=HD×![]() =4×
=4×![]() =
=![]() ,
,
∵EF垂直平分AD,AB⊥AD,
∴HF是△ABD的中位线,
∴HF=![]() AB=
AB=![]() ×6=3,
×6=3,
∴EF=EH+HF=![]() +3=
+3=![]() .
.

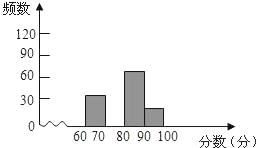
【题目】为迎接国庆60周年,某校举行以“祖国成长我成长”为主题的图片制作比赛,赛后整理参赛同学的成绩,并制作成图表如下:
分数段 | 频数 | 频率 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | m | 0.45 |
80≤x<90 | 60 | n |
90≤x<100 | 20 | 0.1 |
请根据以上图表提供的信息,解答下列问题:
(1)表中m和n所表示的数分别为:m= ,n= ;
(2)请在图中,补全频数分布直方图;
(3)比赛成绩的中位数落在哪个分数段;
(4)如果比赛成绩80分以上(含80分)可以获得奖励,那么获奖率是多少?