题目内容
【题目】如图,在![]() 中,AB为
中,AB为![]() 的直径,C为
的直径,C为![]() 上一点,P是
上一点,P是![]() 的中点,过点P作AC的垂线,交AC的延长线于点D.
的中点,过点P作AC的垂线,交AC的延长线于点D.
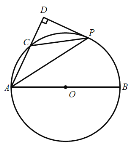
(1)求证:DP是![]() 的切线;
的切线;
(2)若AC=5,![]() ,求AP的长.
,求AP的长.
【答案】(1)见解析;(2)AP=![]() .
.
【解析】
(1)根据题意连接OP,直接利用切线的定理进行分析证明即可;
(2)根据题意连接BC,交于OP于点G,利用三角函数和勾股定理以及矩形的性质进行综合分析计算即可.
解:(1)证明:连接OP;
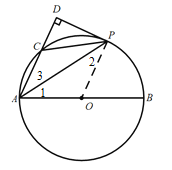
∵OP=OA;
∴∠1=∠2;
又∵P为![]() D的中点;
D的中点;
∴![]()
∴∠1=∠3;
∴∠3=∠2;
∴OP∥DA;
∵∠D=90°;
∴∠OPD=90°;
又∵OP为O半径;
∴DP为O的切线;
(2)连接BC,交于OP于点G;
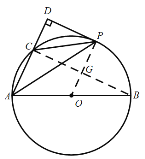
∵AB是圆O的直径;
∴∠ACB为直角;
∵![]()
∴sin∠ABC=![]()
AC=5,则AB=13,半径为![]()
由勾股定理的BC=![]() ,那么CG=6
,那么CG=6
又∵四边形DCGP为矩形;
∴GP=DC=6.5-2.5=4
∴AD=5+4=9;
在Rt△ADP中,AP=![]() .
.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目