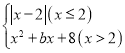题目内容
【题目】发现与探索．
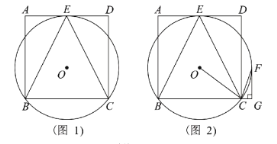
（1）根据小明的解答（图1）分解因式（a-1）2-8（a-1）+7
（2）根据小丽的思考（图2）解决问题，说明：代数式a2-12a+20的最小值为-16．
（3）求代数式-a2+12a-8的最大值．
【答案】（1）
；（2）说明见解析；（3）最大值为28．
【解析】
（1）先配成完全平方式与一个平方数差的形式，再运用平方差公式进行因式分解即可；
（2）依据小丽的思路通过配方进行证明即可；
（3）原式先提取“-”，再通过配方，得-（a-6）2+28，根据-（a-6）2≤0可得解
（1）（a-1）2-8（a-1）+7
=（a-1）2-8（a-1）+16-16+7
=（a-5）2-32
=（a-8）（a-2）；
（2）a2-12a+20
=a2-12a+36-36+20
=（a-6）2-16
∵无论a取何值（a-6）2≥0
∴代数式（a-6）2-16≥-16，
∴a2-12a+20的最小值为-16；
（3）-a2+12a-8．
=-（a2-12a+8）
=-（a2-12a+36-36+8）
=-（a-6）2+36-8
=-（a-6）2+28
∵a取何值-（a-6）2≤0，
∴代数式-（a-6）2+28≤28
∴-a2+12a-8的最大值为28．
【题目】数学兴趣小组经过市场调查，得到某种运动服每月的销量与售价的相关信息如下表：
售价（元/件） | 100 | 110 | 120 | 130 | … |
月销量（件） | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件60元．
（1）销售该运动服每件的利润是多少元；（用含
的式子表示）
（2）求月销量
与售价的关系式；
（3）设销售该运动服的月利润为
元，那么售价为多少时，当月的利润最大，最大利润是多少？
【题目】
年
月
日是第
个世界读书日，这一天世界各地都会举办诸多与阅读有关的活动．某书店为了迎接“读书节”制定了活动计划，以下是活动计划书的部分信息．
“读书节”活动计划书 | ||
书本类别 |
|
|
进价(单位：元) | 18 | 12 |
备注 | 用不超过16800元购进
| |
(1)陈经理查看计划书发现：
类图书的标价是
类图书标价的
倍，若顾客用
元购买图书，能单独购买类图书的数量恰好比单独购买类图书的数量少
本．请求出、两类图书的标价．
(2)经市场调查后，陈经理发现他们高估了“读书节”对图书销售的影响，便调整了销售方案：
类图书每本按标价降价
元
销售， 类图书价格不变．那么书店应如何进货才能获得最大利润？
