题目内容
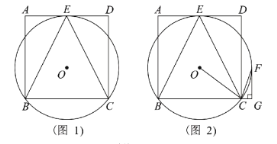
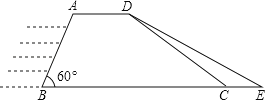
【题目】如图,马边水务部门为加强马边河防汛工作,决定对某水电站水库进行加固.原大坝的横断面是梯形ABCD,如图所示,已知迎水面AB的长为10米,∠B=60°,背水面DC的长度为10![]() 米,加固后大坝的横断面为梯形ABED.若CE的长为4米.
米,加固后大坝的横断面为梯形ABED.若CE的长为4米.
(1)已知需加固的大坝长为120米,求需要填方多少立方米;
(2)求新大坝背水面DE的坡度.(计算结果保留根号)
【答案】(1)需要土石方1200![]() 立方米;(2)背水坡坡度为
立方米;(2)背水坡坡度为![]()
【解析】
(1)分别过A、D作下底的垂线,设垂足为F、G.在Rt△ABF中,已知坡面长和坡角的度数,可求得铅直高度AF的值,也就得到了DG的长;以CE为底,DG为高即可求出△CED的面积,再乘以大坝的长度,即为所需的填方体积;
(2)在Rt△CDG中,由勾股定理求CG的长,即可得到GE的长;Rt△DEG中,根据DG、GE的长即可求得坡角的正切值,即坡面DE的坡比.
解:(1)分别过A、D作AF⊥BC,DG⊥BC,垂点分别为F、G,如图所示.
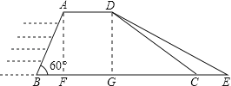
在Rt△ABF中,AB=10米,∠B=60°,sin∠B=![]() ,
,
∴AF=10×![]() =5
=5![]() ,DG=5
,DG=5![]() .
.
∴S△DCE=![]() .
.
需要填方:![]() (立方米);
(立方米);
(2)在直角三角形DGC中,DC=10![]() ,
,
∴GC=![]() ,
,
∴GE=GC+CE=19,
坡度![]()
答:(1)需要土石方1200![]() 立方米.
立方米.
(2)背水坡坡度为![]() .
.

【题目】某校为提高学生体考成绩,对全校300名九年级学生进行一分种跳绳训练.为了解学生训练效果,学校体育组在九年级上学期开学初和学期末分别对九年级学生进行一分种跳绳测试,学生成绩均为整数,满分20分,大于18分为优秀.现随机抽取了同一部分学生的两次成绩进行整理、描述和分析.(成绩得分用x表示,共分成五组:A.x<13,B.13≤x<15,C.15≤x<17,D.17≤x<19,E.19≤x≤20)
开学初抽取学生的成绩在D组中的数据是:17,17,17,17,17,18,18.
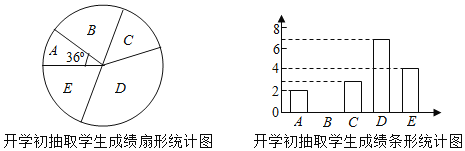
学期末抽取学生成绩统计表
学生成绩 | A组 | B组 | C组 | D组 | E组 |
人数 | 0 | 1 | 4 | 5 | a |
分析数据:
平均数 | 中位数 | 众数 | |
开学初抽取学生成绩 | 16 | b | 17 |
学期末抽取学生成绩 | 18 | 18.5 | 19 |
根据以上信息,解答下列问题:
(1)直接写出图表中a、b的值,并补全条形统计图;
(2)假设该校九年级学生都参加了两次测试,估计该校学期末成绩优秀的学生人数比开学初成绩优秀的学生人数增加了多少?
(3)小莉开学初测试成绩16分,学期末测试成绩19分,根据抽查的相关数据,请选择一个合适的统计量评价小莉的训练效果.