Question

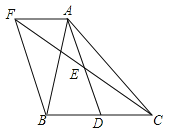
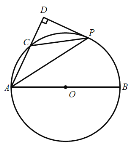
【题目】已知：如图，在直角三角形ABC中，∠ACB=90°，BC的垂直平分线交BC点D，交AB于点E，过点A作AF∥CE交直线DE于点F．

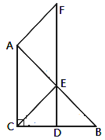
（1）求证：四边形ACEF是平行四边形；

（2）当∠B的大小满足什么条件时，四边形ACEF是菱形？请证明你的结论；

（3）四边形ACEF有可能是矩形吗？请说明理由．

Answer 1

【答案】（1）见解析；（2）当∠B=30°时，四边形ACEF是菱形，见解析；（3）不可能是矩形，见解析

【解析】

（1）根据DF为BC垂直平分线，得出BD=CD，DF⊥BC，根据∠ACB=∠BDF=90°得出DF∥AC，结合AF∥CE，从而得到平行四边形；

（2）当∠B=30°时，AC=AB，CE=AB，从而得到AC=CE，得到菱形；

（3）根据CE在△ABC内部，∠ACE＜∠ACB=90°，则不可能为正方形．

解：（1）证明：∵ED是BC的垂直平分线，

∴DF⊥BC

∴∠FDB=90°

∵∠ACB=90°

∴AC∥DF

∵AF∥CE

∴四边形ACEF是平行四边形

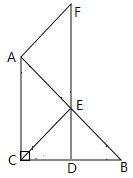
（2） 解：当∠B=30°时，四边形ACEF是菱形．证明如下：

∵∠B=30°，∠ACB=90°，

∴

∵ED是BC的垂直平分线 ∠ACB=90°

∴

∴EC=AC

∵由（1）得四边形ACEF是平行四边形

∴四边形ACEF是菱形

（3）四边形ACEF不可能是矩形．理由如下：

假如，四边形ACEF是矩形，则有∠ACE=90°

而∠ACE＜90°

∴四边形ACEF不可能是矩形．