题目内容
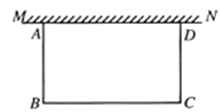
【题目】如图1,我们知道,若点![]() 将线段
将线段![]() 分成两部分,且
分成两部分,且![]() ,则称点
,则称点![]() 为线段
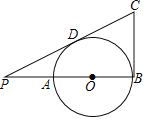
为线段![]() 的黄金分割点.类似的,我们把有一个内角等于
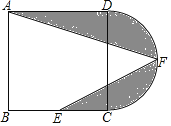
的黄金分割点.类似的,我们把有一个内角等于![]() 的等腰三角形称为黄金三角形,如图
的等腰三角形称为黄金三角形,如图![]() ,
,![]() 是
是![]() 的直径,点
的直径,点![]() 在
在![]() 上,
上,![]() ,过点
,过点![]() 作直线
作直线![]() 分别交直线
分别交直线![]() 和
和![]() 于点
于点![]() 、
、![]() ,连接
,连接![]() ,
,![]() .
.
(1)求![]() 的度数,并证明
的度数,并证明![]() 是黄金三角形;
是黄金三角形;
(2)求证:点![]() 是线段
是线段![]() 的黄金分割点;
的黄金分割点;
(3)对于实数:![]() ,如果满足
,如果满足![]() ,
,![]()
![]() 则称
则称![]() 为
为![]() ,
,![]() 的黄金数,
的黄金数,![]() 为
为![]() ,
,![]() 的白银数.
的白银数.
①实数![]() ,且
,且![]() 为
为![]() ,1的黄金数,
,1的黄金数,![]() 为
为![]() ,1的白银数,求
,1的白银数,求![]() 的值.
的值.
②实数![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,t的黄金数和白银数,求
,t的黄金数和白银数,求![]() 的值.
的值.

【答案】(1)![]() ,
,![]() 是黄金三角形证明见解析;(2)证明见解析;(3)①
是黄金三角形证明见解析;(2)证明见解析;(3)①![]() ;②
;②![]() 或
或![]()
【解析】
(1)由题意,根据同圆半径相等和三角形内角和,可求![]() 的度数,再由黄金三角形定义可证明
的度数,再由黄金三角形定义可证明![]() 是黄金三角形;
是黄金三角形;
(2)由(1)条件证明![]() ,再由黄金分割定义问题可证明;
,再由黄金分割定义问题可证明;
(3)①根据黄金数和白银数的定义,分别求出对应的a、b的值,则问题可解;
②根据k的正负取值,根据定义分别用k表示m、n,再求出比值即可.
(1)![]() 是⊙
是⊙![]() 的直径,
的直径,![]() ,
,
![]() ,则
,则![]() ,
,
设![]() ,则
,则![]() ,
,
又![]()
![]()
![]()
![]() .
.
则![]()
![]()
![]()
又![]()
![]() 是黄金三角形.
是黄金三角形.
(2)由(1)得,![]()
![]()
![]()
![]()
![]() ,
,
又![]()
![]()
![]() 点
点![]() 是线段
是线段![]() 的黄金分割点.
的黄金分割点.
(3)①![]() 为
为![]() 的黄金数,且实数
的黄金数,且实数![]()
![]()
![]()
![]() (舍),
(舍),![]()
![]() 为
为![]() 的白银数,且实数
的白银数,且实数![]()
![]()
![]()
![]() (舍)
(舍)![]()
②![]() 分别为
分别为![]() 的黄金数和白银数,实数
的黄金数和白银数,实数![]()
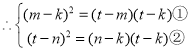
分两种情况:i)当![]() 时,
时,![]()
由①得:![]()
![]()
![]()
由②得:![]()
![]()
![]()
![]()
![]()
ii)当![]() 时,
时,![]() ,由①得:
,由①得:
![]()
![]()
![]()
由②得:![]()
![]()
![]()
![]()
![]()
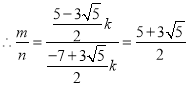
综上, ![]() 的值是
的值是![]() 或
或![]()

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
【题目】数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
售价(元/件) | 100 | 110 | 120 | 130 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件60元.
(1)销售该运动服每件的利润是多少元;(用含![]() 的式子表示)
的式子表示)
(2)求月销量![]() 与售价
与售价![]() 的关系式;
的关系式;
(3)设销售该运动服的月利润为![]() 元,那么售价为多少时,当月的利润最大,最大利润是多少?
元,那么售价为多少时,当月的利润最大,最大利润是多少?