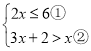题目内容
【题目】某水果商计划购进甲、乙两种水果进行销售,经了解,甲种水果的进价比乙种水果的进价每千克少4元,且用800元购进甲种水果的数量与用1000元购进乙种水果的数量相同.
(1)求甲、乙两种水果的单价分别是多少元?
(2)该水果商根据该水果店平常的销售情况确定,购进两种水果共200千克,其中甲种水果的数量不超过乙种水果数量的3倍,且购买资金不超过3420元,购回后,水果商决定甲种水果的销售价定为每千克20元,乙种水果的销售价定为每千克25元,则水果商应如何进货,才能获得最大利润,最大利润是多少?
【答案】(1)甲、乙两种水果的单价分别是16元、20元;(2)水果商进货甲种水果145千克,乙种水果55千克,才能获得最大利润,最大利润是855元.
【解析】
(1)根据题意可以列出相应的分式方程,求出甲、乙两种水果的单价分别是多少元;
(2)根据题意可以得到利润和购买甲种水果数量之间的关系,再根据甲种水果的数量不超过乙种水果数量的3倍,且购买资金不超过3420元,可以求得甲种水果数量的取值范围,最后根据一次函数的性质即可解答本题.
(1)设甲种水果的单价是x元,则乙种水果的单价是![]() 元,
元,
![]() ,
,
解得,![]() ,
,
经检验,![]() 是原分式方程的解,
是原分式方程的解,
∴![]() ,
,
答:甲、乙两种水果的单价分别是16元、20元;
(2)设购进甲种水果a千克,则购进乙种水果![]() 千克,利润为w元,
千克,利润为w元,
![]() ,
,
∵甲种水果的数量不超过乙种水果数量的3倍,且购买资金不超过3420元,
∴![]() ,
,
解得,![]() ,
,
∴当![]() 时,w取得最大值,此时
时,w取得最大值,此时![]() ,
,![]() ,
,
答:水果商进货甲种水果145千克,乙种水果55千克,才能获得最大利润,最大利润是855元.

【题目】为倡导健康环保,自带水杯已成为一种好习惯,某超市销售甲,乙两种型号水杯,进价和售价均保持不变,其中甲种型号水杯进价为25元/个,乙种型号水杯进价为45元/个,下表是前两月两种型号水杯的销售情况:
时间 | 销售数量(个) | 销售收入(元)(销售收入=售价×销售数量) | |
甲种型号 | 乙种型号 | ||
第一月 | 22 | 8 | 1100 |
第二月 | 38 | 24 | 2460 |
(1)求甲、乙两种型号水杯的售价;
(2)第三月超市计划再购进甲、乙两种型号水杯共80个,这批水杯进货的预算成本不超过2600元,且甲种型号水杯最多购进55个,在80个水杯全部售完的情况下设购进甲种号水杯a个,利润为w元,写出w与a的函数关系式,并求出第三月的最大利润.