Question

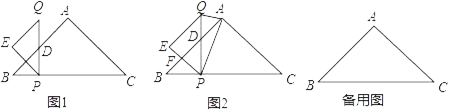
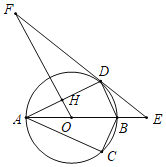
【题目】如图，在Rt△ABC中，∠ACB＝90°，点O为△ABC外接圆的圆心，将△ABC沿AB翻折后得到△ABD．

（1）求证：点D在⊙O上；

（2）在直径AB的延长线上取一点E，使DE2＝BEAE．

①求证：直线DE为⊙O的切线；

②过点O作OF∥BD交AD于点H，交ED的延长线于点F．若⊙O的半径为5，cos∠DBA＝，求FH的长．

Answer 1

【答案】（1）见解析；（2）①见解析；②FH＝．

【解析】

（1）连接OD，由圆周角定理得出AB为直径，由翻折可知△ADB≌△ACB，得出∠ADB=90°，证出OD=AB即可；
（2）①先证明△EBD∽△EDA，得出∠EDB=∠DAE，由等腰三角形的性质得出∠ABD=∠ODB，由∠DAB+∠DBA=90°，得出∠EDB+∠ODB=90°，证出∠EDO=90°，即可得出结论；
②由三角函数得出BD=6，由勾股定理得出AD=8，证出HD=AD=4，由三角形中位线定理得出OH=BD=3，由三角函数求出FO=，即可得出结果．

（1）证明：连接OD，如图所示：

∵∠ACB＝90°，

∴AB为直径，

由翻折可知△ADB≌△ACB，

∴∠ADB＝90°，

∵O为AB中点，

∴OD＝AB，

∴D在⊙O上；

（2）①证明：∵DE2＝BEAE，

∴，∠E＝∠E，

∴△EBD∽△EDA，

∴∠EDB＝∠DAE，

∵OD＝OB，

∴∠ABD＝∠ODB，

∵∠ADB＝90°，

∴∠DAB+∠DBA＝90°，

∴∠EDB+∠ODB＝90°，

∴∠EDO＝90°，

∴DE为⊙O切线；

②解：在Rt△ADB中，∵cos∠DBA＝，AB＝10，

∴BD＝6，

∴AD＝＝8，

∵∠ADB＝90°，OF∥BD，

∴∠FHD＝∠ADB＝90°，

∵OH⊥AD，

∴HD＝AD＝4，

又∵OA＝OB，

∴OH＝BD＝3，

∵∠HOD＝∠ODB＝∠ABD，

∴cos∠HOD＝，

即

∴FO＝，

∴FH＝FO﹣HO＝