题目内容
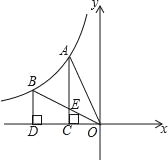
【题目】如图,反比例函数y=![]() (k≠0)的图象经过A,B两点,过点A作AC⊥x轴,垂足为C,过点B作BD⊥x轴,垂足为D,连接AO,连接BO交AC于点E,若OC=CD,四边形BDCE的面积为2,则k的值为( )
(k≠0)的图象经过A,B两点,过点A作AC⊥x轴,垂足为C,过点B作BD⊥x轴,垂足为D,连接AO,连接BO交AC于点E,若OC=CD,四边形BDCE的面积为2,则k的值为( )
A. ﹣![]() B. ﹣
B. ﹣![]() C. ﹣
C. ﹣![]() D. ﹣
D. ﹣![]()
【答案】C
【解析】
先设点B坐标为(a,b),根据平行线分线段成比例定理,求得梯形BDCE的上下底边长与高,再根据四边形BDCE的面积求得ab的值,最后计算k的值.
解:设点B坐标为(a,b),则DO=﹣a,BD=b
∵AC⊥x轴,BD⊥x轴
∴BD∥AC
∵OC=CD
∴CE=![]() BD=
BD=![]() b,CD=
b,CD=![]() DO=
DO=![]() a
a
∵四边形BDCE的面积为2
∴![]() (BD+CE)×CD=2,即
(BD+CE)×CD=2,即![]() (b+
(b+![]() b)×(﹣
b)×(﹣![]() a)=2
a)=2
∴ab=﹣![]()
将B(a,b)代入反比例函数y=![]() (k≠0),得
(k≠0),得
k=ab=﹣![]()
故选:C.


练习册系列答案
相关题目