Question

【题目】如图，在Rt△ABC中，∠A＝90°，AB＝AC＝4．一动点P从点B出发，沿BC方向以每秒1个单位长度的速度匀速运动，到达点C即停止，在整个运动过程中，过点P作PD⊥BC与Rt△ABC的直角边相交于点D，延长PD至点Q，使得PD＝QD，以PQ为斜边在PQ左侧作等腰直角三角形PQE．设运动时间为t秒（t＞0）

（1）在整个运动过程中，判断PE与AB的位置关系是

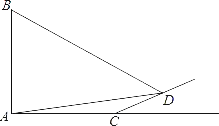
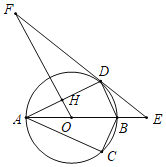
（2）如图2，当点D在线段AB上时，连接AQ、AP，是否存在这样的b，使得AP＝PQ？若存在，求出对应的t的值；若不存在，请说明理由；

（3）当t＝4时，点D经过点A：当t＝时，点E在边AB上．设△ABC与△PQE重叠部分的面积为S，请求出在整个运动过程中S与t之间的函数关系式，以及写出相应的自变量t的取值范围，并求出当4＜t≤时S的最大值．

Answer 1

【答案】（1）PE与AB互相垂直，理由详见解析；（2）t的值为；（3）详见解析.

【解析】

（1）结论：PE与AB互相垂直．理由等腰直角三角形的性质即可证明．

（2）如图2中，过点A作AH⊥BC于点H．根据AP＝PQ，构建方程即可解决问题．

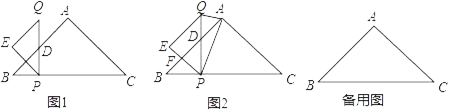
（3）分三种情形：①如图3﹣1中，当0＜t≤4时．△ABC与△PQE的重叠部分为△PFD．②如图3﹣2中，当4＜t≤时，△ABC与△PQE的重叠部分为四边形PDAF．③如图3﹣3中，当＜t≤8时，△ABC与△PQE的重叠部分为四边形FEPD．分别求解即可．

解：（1）结论：PE与AB互相垂直．

理由：如图1中，设PE交AB于K．

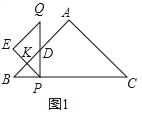
∵△ABC，△PQE都是等腰直角三角形，

∴∠B＝∠EPQ＝45°，

∵PQ⊥BC，

∴∠BPQ＝90°，

∴∠EPB＝90°，

∴∠B+∠EPB＝90°，

∴∠PKB＝90°，

∴PE⊥AB．

（2）如图2中，过点A作AH⊥BC于点H．

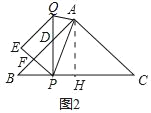
∵Rt△ABC中，AB＝AC＝4

∴BC＝＝8，

∴AH＝BH＝CH＝4，

依题意得BP＝t．PH＝BH﹣BP＝4﹣t，

∴PA＝＝，

∵PD⊥BC，∠B＝45°，

∴PD＝BP＝t，PQ＝2PD＝2t，

∵PQ＝AP，

∴2t＝，

解得：t＝或（舍弃），

∴t的值为．

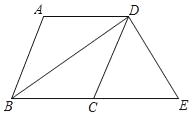
（3）如图3﹣1中，△ABC与△PQE的重叠部分为△PFD．

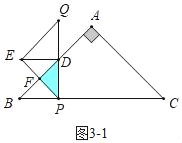
由题意可得△PFD、△BPD为等腰直角三角形，

∴BP＝PD＝t，

∴PF＝DF＝PDcos45°＝t，

∴S＝PFDF＝（0＜t≤4）．

如图3﹣2中，△ABC与△PQE的重叠部分为四边形PDAF．

由题意可得△PFB、△PDC为等腰直角三角形，

∵BP＝t，PC＝BC﹣PB＝8﹣t，

∴BF＝PF＝t，DP＝PC＝8﹣t，

∴S＝S△ABC﹣S△PFB﹣S△PDC

＝×4×4﹣×t×t﹣（8﹣t）（8﹣t）

＝﹣t2+8t﹣16（4＜t≤）

＝﹣（t﹣）2+

∵﹣＜0，

∴当x＝时，S有最大值．

如图3﹣3中，△ABC与△PQE的重叠部分为四边形FEPD．

∵CP＝PD＝8﹣t，

∴QD＝PD＝8﹣t，PQ＝16﹣2t，

由题意可得△QDF为等腰直角三角形

∴QF＝（8﹣t），QE＝（16﹣2t），

∴S＝S△PQE﹣S△QDF

＝×（16﹣2t）（16﹣2t）﹣×（8﹣t）×（8﹣t）

＝﹣12t+48（＜t≤8）．