题目内容
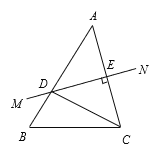
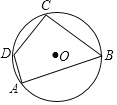
【题目】如图,四边形ABCD内接于⊙O,AB=17,CD=10,∠A=90°,cosB=![]() ,求AD的长.
,求AD的长.
【答案】AD=6.
【解析】根据圆内接四边形的对角互补得出∠C=90°,∠ABC+∠ADC=180°.作AE⊥BC于E,DF⊥AE于F,则CDFE是矩形,EF=CD=10.解Rt△AEB,得出BE=ABcos∠ABE=![]() ,AE=
,AE=![]() ,那么AF=AE-EF=
,那么AF=AE-EF=![]() .再证明∠ABC+∠ADF=90°,根据互余角的互余函数相等得出sin∠ADF=cos∠ABC=
.再证明∠ABC+∠ADF=90°,根据互余角的互余函数相等得出sin∠ADF=cos∠ABC=![]() .解Rt△ADF,即可求出AD=
.解Rt△ADF,即可求出AD=![]() =6.
=6.
∵四边形ABCD内接于⊙O,∠A=90°,
∴∠C=180°-∠A=90°,∠ABC+∠ADC=180°.
作AE⊥BC于E,DF⊥AE于F,则CDFE是矩形,EF=CD=10.
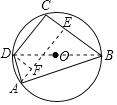
在Rt△AEB中,∵∠AEB=90°,AB=17,cos∠ABC=![]() ,
,
∴BE=ABcos∠ABE=![]() ,
,
∴AE=![]() ,
,
∴AF=AE-EF=![]() .
.
∵∠ABC+∠ADC=180°,∠CDF=90°,
∴∠ABC+∠ADF=90°,
∵cos∠ABC=![]() ,
,
∴sin∠ADF=cos∠ABC=![]() .
.
在Rt△ADF中,∵∠AFD=90°,sin∠ADF=![]() ,
,
∴AD= .
.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
【题目】 在建设社会主义新农村过程中,某村委决定投资开发项目,现有6个项目可供选择,各项目所需资金及预计年利润如下表:
所需资金(亿元) | 1 | 2 | 4 | 6 | 7 | 8 |
预计利润(千万元) | 0.2 | 0.35 | 0.55 | 0.7 | 0.9 | 1 |
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果预计要获得0.9千万元的利润,你可以怎样投资项目?
(3)如果该村可以拿出10亿元进行多个项目的投资,预计最大年利润是多少?说明理由.