题目内容
【题目】已知二次函数y=kx2(k3)x3在x=0和x=4时的函数值相等.
(1)求该二次函数的表达式;
(2)画出该函数的图象,并结合图象直接写出当y<0时,自变量x的取值范围;
(3)已知关于x的一元二次方程![]() ,当1≤m≤3时,判断此方程根的情况.
,当1≤m≤3时,判断此方程根的情况.
【答案】(1)![]() .
.
【解析】
试题(1)由二次函数在![]() 和
和![]() 时的函数值相等,可以得到对称轴为
时的函数值相等,可以得到对称轴为![]() ,即可求出K的值;
,即可求出K的值;
(2)作出二次函数的图象,根据图象可以求出当![]() 时,自变量
时,自变量![]() 的取值范围;
的取值范围;
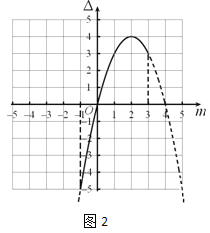
(3)由(1)得,k=1,此方程的判别式△=![]() . 作出图象,由图象得出结论.
. 作出图象,由图象得出结论.
试题解析:(1) 由题意可知,此二次函数图象的对称轴为![]() ,即
,即![]() .∴
.∴![]() .∴
.∴![]() ;
;
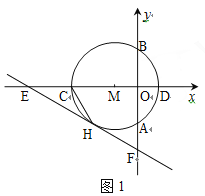
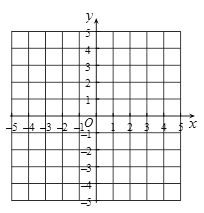
(2)如图1,

由图象可得:当1<x<3时,![]() ;
;
(3)由(1)得此方程为![]() ,
,![]() =
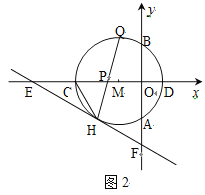
=![]() . ∴Δ是m的二次函数.由图2可知,当-1≤m<0时,Δ<0;当m=0时,Δ=0;当0<m≤3时,Δ>0.∴当-1≤m<0时,原方程没有实数根;当m=0时,原方程有两个相等的实数根 ;当0<m≤3时,原方程有两个不相等的实数根.
. ∴Δ是m的二次函数.由图2可知,当-1≤m<0时,Δ<0;当m=0时,Δ=0;当0<m≤3时,Δ>0.∴当-1≤m<0时,原方程没有实数根;当m=0时,原方程有两个相等的实数根 ;当0<m≤3时,原方程有两个不相等的实数根.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目