题目内容
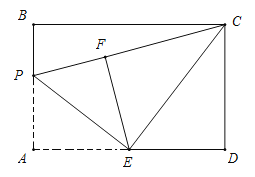
【题目】如图,矩形![]() 的周长是20,且
的周长是20,且![]() ,
,![]() 是
是![]() 边上的中点,点
边上的中点,点![]() 是
是![]() 边上的一个动点,将
边上的一个动点,将![]() 沿
沿![]() 折叠得到
折叠得到![]() ,连接
,连接![]() ,
,![]() ,当
,当![]() 是直角三角形时,
是直角三角形时,![]() 的长是______.
的长是______.
【答案】![]() 或3
或3
【解析】
分两种情况进行讨论:当∠CFE=90°时,△ECF是直角三角形;当∠CEF=90°时,△ECF是直角三角形,分别根据直角三角形的勾股定理列方程求解即可.
∵矩形ABCD的周长是20,
∴AD+CD=10
∵AD:CD=3:2,
∴AD=6,CD=4,
如图所示,当∠CFE=90°时,△ECF是直角三角形,
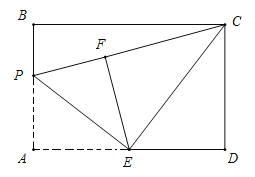
由折叠可得,∠PFE=∠A=90°,AE=FE=DE,
∴∠CFP=180°,即点P,F,C在一条直线上,
在Rt△CDE和Rt△CFE中,
![]() ,
,
∴Rt△CDE≌Rt△CFE(HL),
∴CF=CD=4,
设AP=FP=x,则BP=4-x,CP=x+4,
在Rt△BCP中,BP2+BC2=PC2,即(4-x)2+62=(x+4)2,
解得x=![]() ,即AP=
,即AP=![]() ;
;
如图所示,当∠CEF=90°时,△ECF是直角三角形,
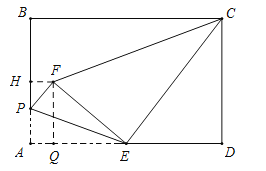
过F作FH⊥AB于H,作FQ⊥AD于Q,则∠FQE=∠D=90°,
又∵∠FEQ+∠CED=90°=∠ECD+∠CED,
∴∠FEQ=∠ECD,
∴△FEQ∽△ECD,
∴![]() ,即
,即![]() ,
,
解得FQ=![]() ,QE=
,QE=![]() ,
,
∴AQ=HF=![]() ,AH=
,AH=![]() ,
,
设AP=FP=x,则HP=![]() -x,
-x,
∵Rt△PFH中,HP2+HF2=PF2,即(![]() -x)2+(
-x)2+(![]() )2=x2,
)2=x2,
解得x=1,即AP=1.
综上所述,AP的长为1或![]() .
.

练习册系列答案
相关题目