题目内容
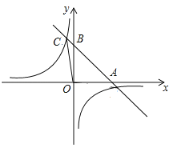
【题目】如图，在平面直角坐标系中，将
绕点
顺时针旋转到
的位置，点
，
分别落在点
，
处，点在
轴上，再将绕点顺时针旋转到
的位置，点
在轴上，将绕点顺时针旋转到
的位置，点
在轴上，依次进行下去……，若点
，
，则点
的坐标为________．
【答案】（10100，4）
【解析】
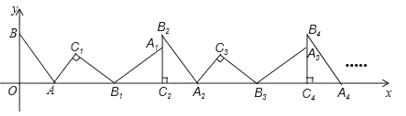
首先根据已知求出三角形三边长度，然后通过旋转发现，B、B2、B4…每偶数之间的B相差10个单位长度，根据这个规律可以求得B2020的坐标．
解：∵AO=
，BO=4，
∴AB=
，
∴OA+AB1+B1C2=
+4=10，
∴B2的横坐标为：10，且B2C2=4，
∴B4的横坐标为：2×10=20，
∴点B2020的横坐标为：1010×10=10100．
∴点B2020的纵坐标为：4．
故点B2020的坐标为（10100，4）．
故答案为：（10100，4）．
练习册系列答案
相关题目
【题目】某超市销售一种商品，成本每千克40元，规定每千克售价不低于成本，且不高于80元，经市场调查，每天的销售量y（千克）与每千克售价x（元）满足一次函数关系，部分数据如下表：
售价x（元/千克） | 50 | 60 | 70 |
销售量y（千克） | 100 | 80 | 60 |
（1）求y与x之间的函数表达式；
（2）设商品每天的总利润为W（元），求W与x之间的函数表达式（利润＝收入﹣成本）；并求出售价为多少元时获得最大利润，最大利润是多少？
