题目内容
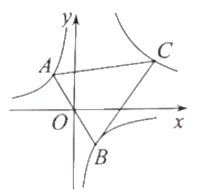
【题目】如图,等腰三角形![]() 的三个顶点分别落在反比例函数
的三个顶点分别落在反比例函数![]() 与
与![]() 的图象上,并且底边
的图象上,并且底边![]() 经过原点
经过原点![]() ,则
,则![]() __________.
__________.
【答案】![]()
【解析】
根据反比例函数图象的对称性可得OA=OB,根据等腰三角形三线合一可证明△AOE∽△OCF,根据相似三角形面积比等于相似比的平方可得![]() ,由勾股定理得出
,由勾股定理得出![]() 即可求得结果.
即可求得结果.
解:∵函数![]() 图象关于原点对称, ∴OA=OB,
图象关于原点对称, ∴OA=OB,
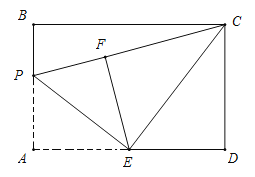
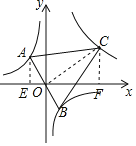
连接OC,过A作AE⊥x轴于E,过C作CF⊥x轴于F,
∵△ABC是底边为AB的等腰三角形,
∴AO⊥OC, ∴∠AOC=90°,
∵AE⊥x轴,CF⊥x轴,
∴∠AEO=∠OFC=∠AOE+∠OAE=90°,
∴∠COF=∠OAE,
∴△AOE∽△OCF,
∴ ![]()
∵顶点A在函数y=![]() 图象的分支上,
图象的分支上,
顶点C在函数y=![]() 图象的分支上
图象的分支上
∴S△AOE=![]() ,S△OCF=
,S△OCF=![]() ,
,
∴ ![]() 即
即![]() ,
,
在Rt△AOC中,AC=![]()
∴cos∠A= ![]() =
= ![]()
故答案为![]()

练习册系列答案
相关题目
【题目】小夏同学从家到学校有![]() ,
,![]() 两条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
两条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
公交车用时 频数 公交车路线 |
|
|
|
| 总计 |
| 59 | 151 | 166 | 124 | 500 |
| 43 | 57 | 149 | 251 | 500 |
据此估计,早高峰期间,乘坐![]() 线路“用时不超过35分钟”的概率为__________,若要在40分钟之内到达学校,应尽量选择乘坐__________(填
线路“用时不超过35分钟”的概率为__________,若要在40分钟之内到达学校,应尽量选择乘坐__________(填![]() 或
或![]() )线路.
)线路.