题目内容
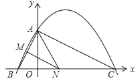
【题目】如图,已知二次函数y=ax2+![]() x+c(a≠0)的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
x+c(a≠0)的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
(1)求出二次函数表达式;
(2)若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时点N的坐标;
(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请求出此时点N的坐标.
【答案】(1) y=﹣![]() x2+
x2+![]() x+4;(2) (3,0);(3)N(﹣8,0)、(8﹣4
x+4;(2) (3,0);(3)N(﹣8,0)、(8﹣4![]() ,0)、(3,0)、(8+4
,0)、(3,0)、(8+4![]() ,0).
,0).
【解析】
(1)根据待定系数法即可求得;
(2)设点N的坐标为(n,0),则BN=n+2,过M点作MD⊥x轴于点D,根据三角形相似对应边成比例求得MD=![]() (n+2),构建二次函数,根据函数解析式求得即可;
(n+2),构建二次函数,根据函数解析式求得即可;
(3)分别以A、C两点为圆心,AC长为半径画弧,与x轴交于三个点,由AC的垂直平分线与x轴交于一个点,即可求得点N的坐标.
解:(1)∵二次函数y=ax2+![]() x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),
x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),
∴![]() ,
,
解得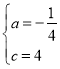 .
.
∴抛物线表达式:![]() ;
;![]()
(2)令y=0,则![]() ,
,
解得x1=8,x2=﹣2,
∴点B的坐标为(﹣2,0).
又∵A(0,4),C(8,0),
∴![]() ,
,
∴AB2+AC2=BC2,
∴∠BAC=90°.
∴AC⊥AB.
∵AC∥MN,
∴MN⊥AB.
设点N的坐标为(n,0),则BN=n+2,
∵MN∥AC,
△BMN∽△BAC
∴![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
∵S△AMN=![]() AMMN
AMMN
=![]()
=![]() ,
,
当n=3时,△AMN面积最大是5,
∴N点坐标为(3,0).
∴当△AMN面积最大时,N点坐标为(3,0).
(3)由(2)知,AC=![]() ,
,
①以A为圆心,以AC长为半径作圆,交x轴于N,此时N的坐标为(﹣8,0),
②以C为圆心,以AC长为半径作圆,交x轴于N,此时N的坐标为(![]() ,0)或(
,0)或(![]() ,0)
,0)
③作AC的垂直平分线交AC于P,交x轴于N,
∴△AOC∽△NPC.
∴![]() 即
即![]() .
.
∴CN=5.
∴此时N的坐标为(3,0),
综上,若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,点N的坐标分别为(﹣8,0)、(![]() ,0)、(3,0)、(
,0)、(3,0)、(![]() ,0).
,0).