题目内容
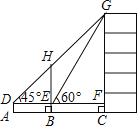
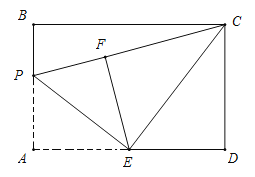
【题目】在平面内由极点、极轴和极径组成的坐标系叫做极坐标系．如图，在平面上取定一点O称为极点；从点O出发引一条射线Ox称为极轴；线段OM的长度称为极径．点M的极坐标就可以用线段OM的长度以及从Ox转动到OM的角度（规定逆时针方向转动角度为正）来确定，即M（4，30°）或M（4，-330°）或M（4，390°）等，则下列说法错误的是（ ）．
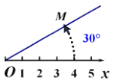
A.点M关于x轴对称点M1的极坐标可以表示为M1（4，-30°）
B.点M关于原点O中心对称点M2的极坐标可以表示为M2（4，570°）
C.以极轴Ox所在直线为x轴建立如图所示的平面直角坐标系，则极坐标M（4，30°）转化为平面直角坐标的坐标为M（2，2
）
D.把平面直角坐标系中的点N（-4，4）转化为极坐标，可表示为N（
，135°）
【答案】C
【解析】
A、B选项，先根据对称的性质确定对称点位置，再得出极坐标；C、D选项，过点M作x轴的垂线，根据勾股定理得出平面直角坐标与极坐标的关系．
A中，点
与点M关于x轴对称，则点在第四象限，极坐标为(4，-30°)
B中，点
与点M关于原点对称，则点在第三象限，极坐标为(4，(30+180)°)，根据极坐标的特点，将角度加360°，结果不变，则可表示为(4，(30+180+360)°)，即(4，570°)；
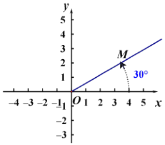
C中，如下图，过点M作x轴的垂线
∵OM=4，∠MON=30°，∴在Rt△MON中，ON=2
，MN=2，∴M(2，2)；
D中，如下图，过点N作x轴的垂线
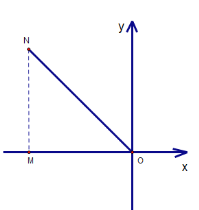
∵N(－4，4)，∴NM=4，MO=4
∴∠NOM=45°，ON=4
，∴∠NOX=135°
∴N(4，135°)
故选：C
华东师大版一课一练系列答案【题目】小夏同学从家到学校有
，
两条不同的公交线路．为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况，在每条线路上随机选取了500个班次的公交车，收集了这些班次的公交车用时（单位：分钟）的数据，统计如下：
公交车用时 频数 公交车路线 |
|
|
|
| 总计 |
| 59 | 151 | 166 | 124 | 500 |
| 43 | 57 | 149 | 251 | 500 |
据此估计，早高峰期间，乘坐线路“用时不超过35分钟”的概率为__________，若要在40分钟之内到达学校，应尽量选择乘坐__________（填或）线路．
