题目内容
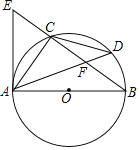
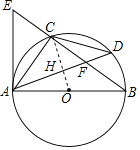
【题目】如图,⊙O是Rt△ABC的外接圆,∠ACB=90°,点D是![]() 上的一点,且
上的一点,且![]() ,连接AD交BC于点F,过点A作⊙O的切线AE交BC的延长线于点E.
,连接AD交BC于点F,过点A作⊙O的切线AE交BC的延长线于点E.
(1)求证:CF=CE;
(2)若AD=8,AC=5,求⊙O的半径.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据切线的性质和圆周角定理得到∠CAE=∠B,∠DAC=∠B,即可得到∠CAE=∠CAF,然后通过证得△CAE≌△CAF即可证得结论;
(2)连接OC,则根据垂径定理得到OC⊥AD,AH=DH,根据勾股定理求得CH=3,设⊙O的半径为r,在Rt△AOH中,OA2=AH2+OH2,得到r2=42+(r﹣3)2,解得即可.
(1)证明:∵∠ACB=90°,
∴AB是⊙O的直径,AC⊥EF,
∵AE是⊙O的切线,
∴∠CAE=∠B,
∵![]() ,
,
∴∠DAC=∠B,
∴∠CAE=∠CAF,
在△CAE和△CAF中
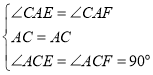
∴△CAE≌△CAF(SAS),
∴CF=CE;
(2)解:连接OC,交AD于H,
∵![]() ,
,
∴OC⊥AD,AH=DH,
∵AD=8,AC=5,
∴AH=4,
在Rt△ACH中,CH=![]() =3,
=3,
设⊙O的半径为r,
∴OH=r﹣3,
在Rt△AOH中,OA2=AH2+OH2,
∴r2=42+(r﹣3)2,
解得r=![]()

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目