题目内容
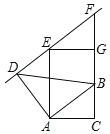
【题目】如图,在 Rt△ABC 中∠C=90°,线段 AD 是线段 AB 绕 A 点按逆时针方向旋转 90°得到的,△EGF 由△ABC 沿 CB 方向平移得到的,且直线 EG 过点 D.
(1)求∠BDF 的大小;
(2)若 AB=10,∠BAC=30°,求 CF 的长.
【答案】(1)45°;(2)5+![]() .
.
【解析】
(1) 由旋转得到AD=AB=10,∠ABD = 45![]() , 由平移可得DF//AB, 即可求出∠BDF=∠ABD=45
, 由平移可得DF//AB, 即可求出∠BDF=∠ABD=45![]() .
.
(2)首先通过AE∥FC,EG∥AC,又∠C=90°可得四边形 ACGE 是矩形, GC=AE,∠EAC=90°,
可证得∠DAE=∠BAC=30°,在 Rt△ADE 中,可得AE的长,又GC=AE,可得CF=CG+FG,可求得CF的长.
解:(1)∵线段 AD 是线段 AB 绕点 A 旋转 90°所得,
∴△ABD 为等腰直角三角形,
∴∠ABD=45°,
由平移知 DF∥AB,
∴∠BDF=∠ABD=45°.
(2)由平移性质可得 AE∥FC,EG∥AC,又∠C=90°,
∴四边形 ACGE 是矩形,
∴GC=AE,∠EAC=90°,
∴∠BAC+∠EAB=90°,又![]() ∠DAE+∠EAB=90°,
∠DAE+∠EAB=90°,
∴∠DAE=∠BAC=30°,
由 DF∥AB 得,![]() ∠EDA+∠DAB=180°,
∠EDA+∠DAB=180°,
∴∠EDA=180°﹣90°=90°,
在 Rt△ADE 中,∵AD=10,∠DAE=30°,
∴AE=![]() =
=![]() ,
,
∴CG=AE=![]() ,
,
∵FG=BC=5,
∴CF=CG+FG=5+![]() .
.

练习册系列答案
相关题目