题目内容
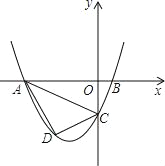
【题目】已知，抛物线y=ax2+3ax+c（a＞0）与y轴交于点C，与x轴交于A，B两点，点A在点B左侧．点B的坐标为（1，0），OC=3OB．
(1)直接写出C点的坐标；
(2)求抛物线的解析式；
(3)若点D是线段AC下方抛物线上的动点，求四边形ABCD面积的最大值．
【答案】(1) （0，﹣3）；(2) y=
x2+
x﹣3；(3) 四边形ABCD面积的最大值为13.5．
【解析】
（1）由点B的坐标为（1，0），OC=3OB，且点C在y轴的负半轴上可求出点C的坐标；
(2)已知了B点坐标,易求得OB、OC的长,进而可将B、C的坐标代入抛物线中,求出待定系数的值,即可得出抛物线的解析式.
(3)根据A、C的坐标,易求得直线AC的解析式.由于AB、OC都是定值,则△ABC的面积不变,若四边形ABCD面积最大,则△ADC的面积最大;可过D作x轴的垂线,交AC于M,x轴于N;易得△ADC的面积是DM与OA积的一半,可设出N点的坐标,分别代入直线AC和抛物线的解析式中,即可求出DM的长,进而可得出四边形ABCD的面积与N点横坐标间的函数关系式,根据所得函数的性质即可求出四边形ABCD的最大面积.
(1)∵点B的坐标为（1，0），OC=3OB，
∴OB=1，OC=3，
∴点C的坐标为（0，﹣3）．
(2)将B（1，0）、C（0，﹣3）代入y=ax2+3ax+c，得：
，解得：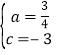
，
∴抛物线的解析式为y=x2+x﹣3．
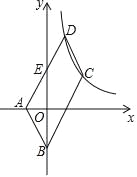
(3)过点D作直线DE∥y轴，交AC于点E，交x轴于点F，过点C作CG⊥DE于点G，如图所示．
当y=0时，有x2+x﹣3=0，
解得：x1=﹣4，x2=1，
∴点A的坐标为（﹣4，0），
∴AB=5．
设直线AC的解析式为y=kx+b（k≠0），
将A（﹣4，0）、C（0，﹣3）代入y=kx+b，得：
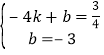，解得：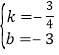
，
∴直线AC的解析式为y=﹣x﹣3．
设点D的坐标为（t，x2+x﹣3），则点E的坐标为（t，﹣ t﹣3），
∴ED=﹣t﹣3﹣（x2+x﹣3）=﹣t2﹣3t，
∴S四边形ABCD=S△ABC+S△AED+S△CED，
=
ABOC+EDAF+EDCG，
=ABOC+EDAO，
=×5×3+×4（﹣t2﹣3t），
=﹣
t2﹣6t+
=﹣（t+2）2+
．
∵﹣＜0，
∴当t=﹣2时，四边形ABCD的面积取最大值，最大值为．
答：四边形ABCD面积的最大值为．
