题目内容
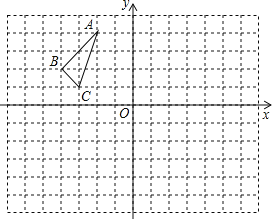
【题目】如图,已知抛物线y=﹣x![]() +bx+c 与y轴相交于点 A(0,3),与x正半轴相交于点B,对称轴是直线 x=1
+bx+c 与y轴相交于点 A(0,3),与x正半轴相交于点B,对称轴是直线 x=1
(1)求此抛物线的解析式以及点B的坐标.
(2)动点M 从点 O 出发,以每秒2个单位长度的速度沿 x 轴正方向运动,同时动点 N 从点O出发,以每秒 3 个单位长度的速度沿y 轴正方向运动,当N点到达 A 点时,M、N同时停止运动.过动点 M 作 x 轴的垂线交线段 AB 于点Q,交抛物线于点 P,设运动的时间为 t 秒.
①当 t 为何值时,四边形 OMPN 为矩形.
②当 t>0 时,△BOQ 能否为等腰三角形?若能,求出 t 的值;若不能,请说明理由.

【答案】(1)y=﹣x![]() +2x+3,B点坐标为(3,0);(2)①当t的值为1时,四边形OMPN为矩形;②当t的值为
+2x+3,B点坐标为(3,0);(2)①当t的值为1时,四边形OMPN为矩形;②当t的值为![]() 或
或![]() 时,△BOQ 为等腰三角形.
时,△BOQ 为等腰三角形.
【解析】
(1)由对称轴公式可求得b,由A点坐标可求得C,则可求得抛物线解析式;再令y=0可求得B点坐标;
(2)①用t可表示出ON和OM,则可表示出P点坐标,即可表示出PM的长,由矩形的性质可得ON=PM,可得到关于的方程,可求得的值;②由题意可知OB=OA,故当△BOQ为等腰三角形时,只能有OB=BQ或OQ=BQ,用t可表示出Q点的坐标,则可表示出OQ和BQ的长,分别得到关于t的方程,可求得t的值.
(1)∵抛物线 y=﹣x![]() +bx+c 对称轴是直线 x=1,
+bx+c 对称轴是直线 x=1,
∴﹣![]() =1,解得 b=2,
=1,解得 b=2,
∵抛物线过 A(0,3),
∴c=3,
∴抛物线解析式为 y=﹣x![]() +2x+3,
+2x+3,
令 y=0 可得﹣x![]() +2x+3=0,解得 x=﹣1 或 x=3,
+2x+3=0,解得 x=﹣1 或 x=3,
∴B 点坐标为(3,0);
(2)①由题意可知 ON=3t,OM=2t,
∵P 在抛物线上,
∴P(2t,﹣4t![]() +4t+3),
+4t+3),
∵四边形 OMPN 为矩形,
∴ON=PM,
∴3t=﹣4t![]() +4t+3,解得 t=1 或 t=﹣
+4t+3,解得 t=1 或 t=﹣![]() (舍去),
(舍去),
∴当 t 的值为 1 时,四边形 OMPN 为矩形;
②∵A(0,3),B(3,0),
∴OA=OB=3,且可求得直线 AB 解析式为 y=﹣x+3,
∴当 t>0 时,OQ≠OB,
∴当△BOQ 为等腰三角形时,有 OB=QB 或 OQ=BQ 两种情况, 由题意可知 OM=2t,
∴Q(2t,﹣2t+3),
∴OQ= ![]() =
=![]() ,BQ=
,BQ=![]() =
=![]() |2t﹣3|, 又由题意可知 0<t<1,
|2t﹣3|, 又由题意可知 0<t<1,
当 OB=QB 时,则有![]() |2t﹣3|=3,解得 t=
|2t﹣3|=3,解得 t=![]() (舍去)或 t=
(舍去)或 t=![]() ;
;
当 OQ=BQ 时,则有![]() =
=![]() |2t﹣3|,解得 t=
|2t﹣3|,解得 t=![]() ;
;
综上可知当 t 的值为![]() 或
或![]() 时,△BOQ 为等腰三角形.
时,△BOQ 为等腰三角形.