题目内容
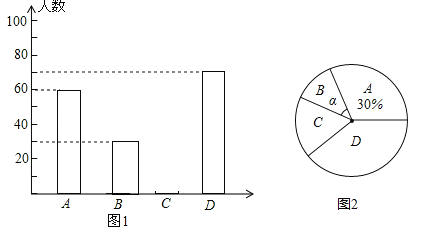
【题目】黔东南州某中学为了解本校学生平均每天的课外学习实践情况,随机抽取部分学生进行问卷调查,并将调查结果分为A,B,C,D四个等级,设学生时间为t(小时),A:t<1,B:1≤t<1.5,C:1.5≤t<2,D:t≥2,根据调查结果绘制了如图所示的两幅不完整的统计图.请你根据图中信息解答下列问题:
(1)本次抽样调查共抽取了多少名学生?并将条形统计图补充完整;
(2)本次抽样调查中,学习时间的中位数落在哪个等级内?
(3)表示B等级的扇形圆心角α的度数是多少?
(4)在此次问卷调查中,甲班有2人平均每天课外学习时间超过2小时,乙班有3人平均每天课外学习时间超过2小时,若从这5人中任选2人去参加座谈,试用列表或化树状图的方法求选出的2人来自不同班级的概率.
【答案】(1)200;(2)C;(3)54°;(4)![]() .
.
【解析】
试题分析:(1)根据B类的人数和所占的百分比即可求出总数;求出C的人数从而补全统计图;
(2)根据中位数定义:将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数可得答案;
(3)用B的人数除以总人数再乘以360°,即可得到圆心角α的度数;
(4)先设甲班学生为A1,A2,乙班学生为B1,B2,B3根据题意画出树形图,再根据概率公式列式计算即可.
试题解析:(1)共调查的中学生数是:80÷40%=200(人),C类的人数是:200﹣60﹣80﹣20=40(人),如图1:
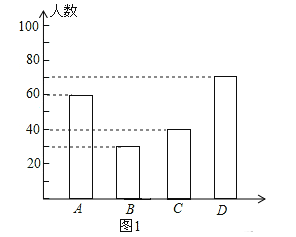
(2)本次抽样调查中,学习时间的中位数落在C等级内;
(3)根据题意得:α=![]() ×360°=54°;
×360°=54°;
(4)设甲班学生为A1,A2,乙班学生为B1,B2,B3,画树状图为:
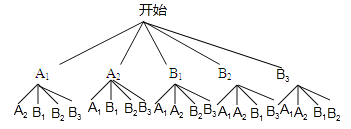
一共有20种等可能结果,其中2人来自不同班级共有12种,∴P(2人来自不同班级)=![]() =
=![]() .
.