题目内容
【题目】如图1,AD∥BC,∠BAD的平分线交BC于点G,∠BCD=90°.
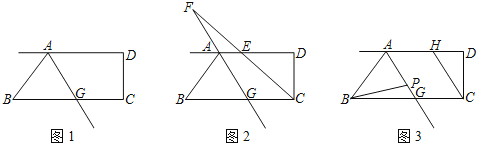
(1)求证:∠BAG=∠BGA;
(2)如图2,若∠ABG=50°,∠BCD的平分线交AD于点E、交射线GA于点F.求∠AFC的度数;
(3)如图3,线段AG上有一点P,满足∠ABP=3∠PBG,过点C作CH∥AG.若在直线AG上取一点M,使∠PBM=∠DCH,请直接写出![]() 的值.
的值.
【答案】(1)详见解析;(2)20°或160°;(3)![]() 的值是5或
的值是5或![]() .
.
【解析】
(1)根据平行线的性质可得∠GAD=∠BGA,然后根据角平分线的定义可得∠BAG=∠GAD,最后利用等量代换即可求出结论;
(2)根据点E在线段AD上和点E在射线DA的延长线上分类讨论,根据画出对应的图形,然后根据角平分线的定义、平行线的性质和等量代换分别求出结论即可;
(3)根据点M在BP下方和BP上方分类讨论,分别画出对应的图形,设∠ABC=4x,
根据平行线的性质、三角形的内角和定理和角平分线的定义分别表示出∠ABM和∠GBM,即可求出结论.
(1)证明:∵AD∥BC,
∴∠GAD=∠BGA,
∵AG平分∠BAD,
∴∠BAG=∠GAD,
∴∠BAG=∠BGA;
(2)解:①若点E在线段AD上,
∵CF平分∠BCD,∠BCD=90°,
∴∠GCF=45°,
∵AD∥BC,
∴∠AEF=∠GCF=45°,
∵∠ABC=50°,
∴∠DAB=180°﹣50°=130°,
∵AG平分∠BAD,
∴∠BAG=∠GAD=65°,
∴∠AFC=65°﹣45°=20°;
②若点E在DA的延长线上,如图4,
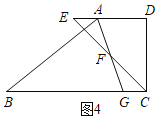
∵∠AGB=65°,∠BCF=45°,
∴∠AFC=∠CGF+∠BCF=115°+45°=160°;
(3)解:有两种情况:
①当M在BP的下方时,如图5,
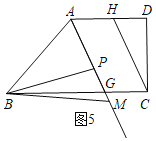
设∠ABC=4x,
∵∠ABP=3∠PBG,
∴∠ABP=3x,∠PBG=x,
∵AG∥CH,
∴∠BCH=∠AGB=![]() =90°﹣2x,
=90°﹣2x,
∵∠BCD=90°,
∴∠DCH=∠PBM=90°﹣(90°﹣2x)=2x,
∴∠ABM=∠ABP+∠PBM=3x+2x=5x,∠GBM=∠PBM-PBG=x
∴∠ABM:∠GBM=5x:x=5;
②当M在BP的上方时,如图6,
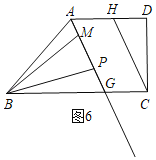
同理得:∠ABM=∠ABP﹣∠PBM=3x﹣2x=x,∠GBM=∠PBG+∠PBM=3x
∴∠ABM:∠GBM=x:3x=![]() .
.
综上,![]() 的值是5或
的值是5或![]() .
.

 优加精卷系列答案
优加精卷系列答案【题目】![]() 市首批一次性投放公共自行车700辆供市民租用出行,由于投入数量不够, 导致出现需要租用却未租到车的现象,现随机抽取的某五天在同一时段的调查数据汇成如下表格.
市首批一次性投放公共自行车700辆供市民租用出行,由于投入数量不够, 导致出现需要租用却未租到车的现象,现随机抽取的某五天在同一时段的调查数据汇成如下表格.
请回答下列问题:
时间 | 第一天7:00﹣8:00 | 第二天7:00﹣8:00 | 第三天7:00﹣8:00 | 第四天7:00﹣8:00 | 第五天7:00﹣8:00 |
需要租用自行车却未租到车的人数(人) | 1500 | 1200 | 1300 | 1300 | 1200 |
(1)表格中的五个数据(人数)的中位数是多少?
(2)由随机抽样估计,平均每天在7:00-8:00 :需要租用公共自行车的人数是多少?