题目内容
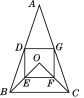
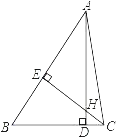
【题目】在△ABC和△DEF中，将△DEF按要求摆放，使得∠D的两条边分别经过点B和点C．
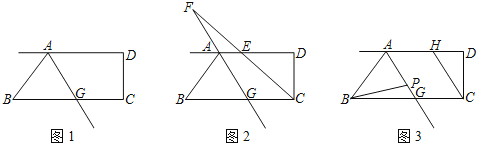
（1）当将△DEF如图1摆放时，若∠A=50°，∠E+∠F=100°，则∠D= ；∠ABD+∠ACD＝ ．
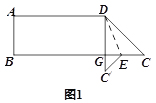
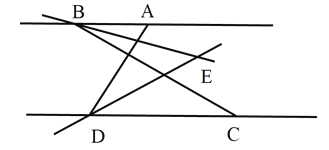
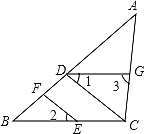
（2）当将△DEF如图2摆放时，∠A=m°，∠E+∠F=n°，请求出∠ABD+∠ACD的度数(用含m、n的代数式表示)．
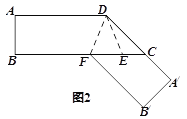
（3）能否将△DEF摆放到某个位置，使得BD、CD同时平分∠ABC和∠ACB．若能，求出∠A、∠E、∠F满足的关系？若不能，请说明理由？
【答案】（1）80°，230°；（2）180°-m°- n°；（3）能，
【解析】
（1）根据三角形内角和可求出∠D的度数，要求∠ABD+∠ACD的度数，只要求出∠ABC+∠CBD+∠ACB+∠BCD，利用三角形内角和定理得出∠ABC+∠ACB=180°-∠A=180°-50°=130°；根据三角形内角和定理，∠CBD+∠BCD=∠E+∠F=100°，得出∠ABD+∠ACD=∠ABC+∠CBD+∠ACB+∠BCD=230°；
（2）要求∠ABD+∠ACD的度数，只要求出∠ABC+∠ACB-（∠BCD+∠CBD）的度数．根据三角形内角和定理，∠CBD+∠BCD=∠E+∠F=n°；根据三角形内角和定理得，∠ABC+∠ACB=180°-∠A=（180-m）°，得出∠ABD+∠ACD=∠ABC+∠ACB-（∠BCD+∠CBD）=（180-m-n）°；
（3）若满足条件，根据题意可得∠ABD+∠ACD＝∠CBD+∠BCD，可得n°＝90°-
m°，从而得出结论.
解：（1）∵∠E+∠F=100°，
∴∠D=180°-（∠E+∠F）=80°，
在△ABC中，∠A+∠ABC+∠ACB=180°，∠A=50°，
∴∠ABC+∠ACB=180°-50°=130°，
在△BCD中，∠D+∠BCD+∠CBD=180°，
∴∠BCD+∠CBD=180°-∠D，
在△DEF中，∠D+∠E+∠F=180°，
∴∠E+∠F=180°-∠D，
∴∠CBD+∠BCD=∠E+∠F=100°，
∴∠ABD+∠ACD=∠ABC+∠CBD+∠ACB+∠BCD=130°+100°=230°；
（2）在△ABC中，∠A+∠ABC+∠ACB=180°，∠A=m°，
∴∠ABC+∠ACB=180°-m°，
在△DEF中，∠D+∠E+∠F=180°，
∴∠D=180°- (∠E+∠F)= 180°-n°，
在△BCD中，∠D+∠BCD+∠CBD=180°，
∴∠BCD+∠CBD=180°-∠D=180°-(180°-n°)= n°，
∴∠ABD+∠ACD
=∠ABC-∠CBD+∠ACB-∠BCD
=(∠ABC+ ACB)-( ∠CBD+∠BCD)
=180°-m°- n°；
（3）能．
∵BD、CD平分∠ABC和∠ACB，
∴∠ABD＝∠CBD，∠ACD＝∠BCD，
∴∠ABD+∠ACD＝∠CBD+∠BCD，
∴180°-m°- n°＝n°，
∴n°＝90°-m°，
∴.
