题目内容
【题目】问题探究：
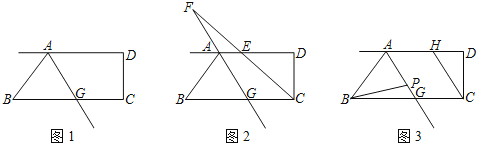
（1）如图①，点M、N分别为四边形ABCD边AD、BC的中点，则四边形BNDM的面积与四边形ABCD的面积关系是 ．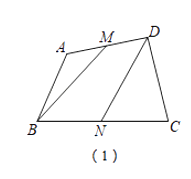 
（2）如图②，在四边形ABCD中，点M、N分别为AD、BC的中点，MB交AN于点P，MC交DN于点Q，若S△四边形MPNQ=10，则S△ABP+S△DCQ的值为多少？
（3）问题解决
在矩形ABCD中，AD=2，DC=4，点M、N为AB上两点，且满足BN=2AM=2MN，连接MC、MD．若点P为CD上任意一点，连接AP、NP，使得AP与DM交于点E，NP与MC交于点F，则四边形MEPF的面积是否存最大值？若存在，请求出最大面积；若不存在，请说明理由．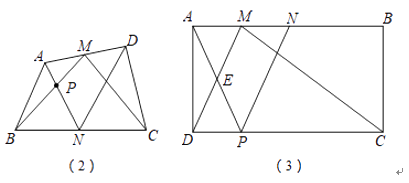
【答案】
（1）S四边形BNDM= 
S四边形ABCD
（2）解：连接BD．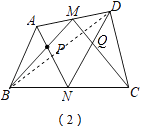 
∵M、N是AD、BC中点，
∴S△ABM=S△BDM，S△BDN=S△CDN，（等底同高的两个三角形面积相等）
∴S四边形BMDN= S四边形ABCD．
同理，S四边形ANCM= S四边形ABCD．
∴S四边形ANCM+S四边形BMDN=S四边形ABCD，
∴S四边形MPNQ=S△ABP+S△CDQ=10；
（3）连接PM，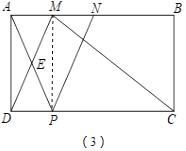 
设DP=x，则PC=4﹣x，
∵AM∥DP，
∴ 
= 
，
∴ 
= 
，即 = 
，
∵ 
= 且S△APM= AMAD=1，
∴S△MPE= ，
同理可得，S△MPF= 
，
∴S= + =2﹣ 
﹣ 
=2﹣ 
=2+ 
≤2﹣ 
= 
，
当x=2时，上式等号成立，
∴S的最大值为： ．
【解析】解：（1）S四边形BNDM= S四边形ABCD，
理由：连接BD， 
∵点M、N分别为四边形ABCD边AD、BC的中点，
∴S△BDM= S△ABD，S△BDN= S△BCD，
∴S四边形BNDM=S△BDM+S△BDN= （S△ABD+S△BCD）= S四边形ABCD，
（2）连接BD．
∵M、N是AD、BC中点，
∴S△ABM=S△BDM，S△BDN=S△CDN，（等底同高的两个三角形面积相等）
∴S四边形BMDN= S四边形ABCD．
同理，S四边形ANCM= S四边形ABCD．
∴S四边形ANCM+S四边形BMDN=S四边形ABCD，
∴S四边形MPNQ=S△ABP+S△CDQ=10；
（3）连接PM，
设DP=x，则PC=4﹣x，
∵AM∥DP，
∴ = ，
∴ = ，即 = ，
∵ = 且S△APM= AMAD=1，
∴S△MPE= 
，
同理可得，S△MPF= ，
∴S= + =2﹣ ﹣ =2﹣ =2+ ≤2﹣ = ，
当x=2时，上式等号成立，
∴S的最大值为： ．
所以答案是：（1）S四边形BNDM= S四边形ABCD；（2）10；（3）存在，最大值为.
