��Ŀ����
����Ŀ������ѧϰ�����Ĺ����뷽����̽������y=![]() ��ͼ�������ʣ�
��ͼ�������ʣ�
��Ϊy=![]() ����y=��
����y=��![]() +1���������ǶԱȺ���y=��
+1���������ǶԱȺ���y=��![]() ��̽����
��̽����
���
x | �� | ��4 | ��3 | ��2 | ��1 | �� |
| 1 | 2 | 3 | 4 | �� |
y=�� | �� |
|
| 1 | 2 | 4 | ��4 | ��1 | 1 | �� | �� | �� |
y= | �� |
|
| 2 | 3 | 5 | ��3 | ��1 | 0 |
|
| �� |
��㣺��ƽ��ֱ������ϵ�У����Ա���x��ȡֵΪ�����꣬��y=![]() ��Ӧ�ĺ���ֵΪ�����꣬�����Ӧ�ĵ㣬��ͼ��ʾ��
��Ӧ�ĺ���ֵΪ�����꣬�����Ӧ�ĵ㣬��ͼ��ʾ��
��1�����y����߸�����ұ߸��㣬�ֱ���һ���⻬����˳������������
��2���۲�ͼ�������ش��������⣺
�ٵ�x��0ʱ��y��x��������� ����������������������С����
��y=![]() ��ͼ������y=��
��ͼ������y=��![]() ��ͼ������ ��ƽ���� ������λ���õ���
��ͼ������ ��ƽ���� ������λ���õ���
��ͼ����ڵ��� �����ĶԳƣ����������꣩
��3����A��x1��y1����B��x2��y2���Ǻ���y=![]() ��ͼ���ϵ����㣬��x1+x2=0������y1+y2+3��ֵ��
��ͼ���ϵ����㣬��x1+x2=0������y1+y2+3��ֵ��
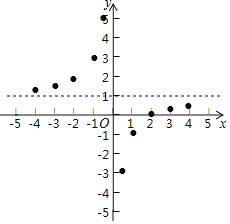
���𰸡�(1)ͼ�����������2�������ϣ�1����0��1������3��5.
����������1���ù⻬����˳�����Ӽ��ɣ�
��2���۲�ͼ������ͼ���ɽ�����⣻
��3���������ĶԳƵ����ʣ���֪A��x1��y1����B��x2��y2�����ڣ�0��1���Գƣ��ɴ˼��ɽ������.
��1������ͼ����ͼ��ʾ��

��2���ٵ�x��0ʱ��y��x�����������
��y=![]() ��ͼ������y=��
��ͼ������y=��![]() ��ͼ������ƽ��1����λ���õ���
��ͼ������ƽ��1����λ���õ���
��ͼ����ڵ㣨0��1�����ĶԳƣ�
�ʴ�Ϊ���������ϣ�1������0��1����
��3����x1+x2=0��
��x1=��x2��
��A��x1��y1����B��x2��y2�����ڣ�0��1���Գƣ�
��y1+y2=2��
��y1+y2+3=5��

 ֱͨ������У�ܲ��¿�ֱͨ��Уϵ�д�
ֱͨ������У�ܲ��¿�ֱͨ��Уϵ�д�