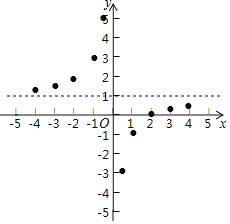题目内容
【题目】乘法公式的探究及应用．
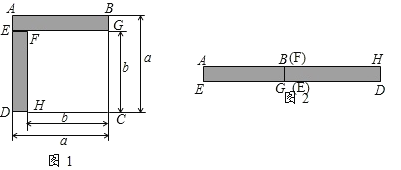
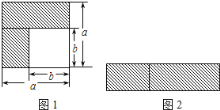
（1）如图1，可以求出阴影部分的面积是______ （写成两数平方差的形式）；
（2）如图2，若将阴影部分裁剪下来，重新拼成一个长方形，它的宽是______，长是______，面积是______．（写成多项式乘法的形式）
（3）比较左、右两图的阴影部分面积，可以得到乘法公式______．（用式子表达）
（4）运用你所得到的公式，计算下列各题：
①10.3×9.7
②（2m+n-p）（2m-n+p）
【答案】（1）a2-b2；（2）a-b；a+b； 
；（3）
；（4）①99.91；②4m2-n2+2np-p2．
【解析】
（1）利用正方形的面积公式就可求出；
（2）仔细观察图形就会知道长，宽，由面积公式就可求出面积；
（3）建立等式就可得出；
（4）利用平方差公式就可方便简单的计算．
解：（1）利用正方形的面积公式可知：阴影部分的面积=a2-b2；
故答案为：a2-b2；
（2）由图可知矩形的宽是a-b，长是a+b，所以面积是（a+b）（a-b）；
故答案为：a-b，a+b，（a+b）（a-b）；
（3）（a+b）（a-b）=a2-b2（等式两边交换位置也可）；
故答案为：（a+b）（a-b）=a2-b2；
（4）①解：原式=（10+0.3）×（10-0.3）
=102-0.32
=100-0.09
=99.91；
②解：原式=[2m+（n-p）][2m-（n-p）]
=（2m）2-（n-p）2
=4m2-n2+2np-p2．
阅读快车系列答案
【题目】参照学习函数的过程与方法，探究函数y=
的图象与性质．
因为y=
，即y=﹣
+1，所以我们对比函数y=﹣来探究．
列表：
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | ﹣ |
| 1 | 2 | 3 | 4 | … |
y=﹣ | … |
|
| 1 | 2 | 4 | ﹣4 | ﹣1 | 1 | ﹣ | ﹣ | … |
y= | … |
|
| 2 | 3 | 5 | ﹣3 | ﹣1 | 0 |
|
| … |
描点：在平面直角坐标系中，以自变量x的取值为横坐标，以y=
相应的函数值为纵坐标，描出相应的点，如图所示：
（1）请把y轴左边各点和右边各点，分别用一条光滑曲线顺次连接起来；
（2）观察图象并分析表格，回答下列问题：
①当x＜0时，y随x的增大而 ；（填“增大”或“减小”）
②y=的图象是由y=﹣的图象向 平移 个单位而得到；
③图象关于点 中心对称．（填点的坐标）
（3）设A（x1，y1），B（x2，y2）是函数y=的图象上的两点，且x1+x2=0，试求y1+y2+3的值．
