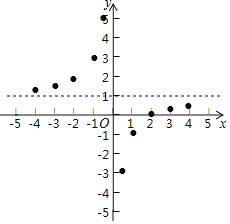题目内容
【题目】如图,P为⊙O外一点,PA、PB分别切⊙O于A、B两点,OP交⊙O于点C,连接BO并延长交⊙O于点D,交PA的延长线于点E,连接AD、BC.下列结论:①AD∥PO;②△ADE∽△PCB;③tan∠EAD=![]() ;④BD2=2ADOP.其中一定正确的是( )
;④BD2=2ADOP.其中一定正确的是( )

A. ①③④ B. ②④ C. ①②③ D. ①②③④
【答案】A
【解析】连接OA,如图,
∵PA、PB分别是O的切线,
∴∠APO=∠BPO,OA⊥PA,OB⊥PB;
∴∠2=∠4,
∵OB=OC,
∴∠1=∠3,
∵∠2++∠4=∠1+∠3,
∴∠3=∠4,
∴OP∥AD,所以①正确;
∵OP∥AD,
∴∠ADE=∠POE,
∵∠POE+∠COB=180°,∠PCB+∠OCB=180°,
而∠COB≠∠OCB,
∴∠PCB≠∠POE,
∴∠PCB≠∠ADE,
∴不能判断△ADE∽△PCB,所以②错误;
∵OP∥AD,
∴∠EAD=∠EPO,![]() ,
,
∴![]() ,
,
在Rt△AOP中,∵tan∠APO=![]() ,
,
而OA=OD,
∴tan∠APO=![]() =
=![]() P,
P,
∴tan∠EAD=![]() ,所以③正确;
,所以③正确;
连结AB,如图,∵BD为直径,
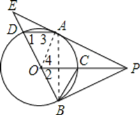
∴∠BAD=90°,
∵OP∥AD,
∴∠ADB=∠POB,
∴Rt△ABD∽△BPO,
∴![]() ,
,
∴![]() BDBD=ADOP,
BDBD=ADOP,
∴BD2=2ADOP,所以④正确。
故选A.

 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案【题目】综合与探究
“十一”黄金周期间,齐齐哈尔市动物园在7天假期中每天接待的人数变化如下表(正数表小比前一天多的人数,负数表示比前一天少的人数):
日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
人数变化(万人) | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
(1)若9月份的最后一天9月30日的游客人数记为![]() 万人,请用含
万人,请用含![]() 的代数式表示10月2日的游客人数;
的代数式表示10月2日的游客人数;
(2)在(1)条件下,请直接写出七天内游客人数最多的是哪天,有多少万人?
(3)若9月30日的游客人数为2万人,门票每人100元,则黄金周期间齐齐哈尔市动物园票收入是多少万元?
【题目】参照学习函数的过程与方法,探究函数y=![]() 的图象与性质.
的图象与性质.
因为y=![]() ,即y=﹣
,即y=﹣![]() +1,所以我们对比函数y=﹣
+1,所以我们对比函数y=﹣![]() 来探究.
来探究.
列表:
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | ﹣ |
| 1 | 2 | 3 | 4 | … |
y=﹣ | … |
|
| 1 | 2 | 4 | ﹣4 | ﹣1 | 1 | ﹣ | ﹣ | … |
y= | … |
|
| 2 | 3 | 5 | ﹣3 | ﹣1 | 0 |
|
| … |
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以y=![]() 相应的函数值为纵坐标,描出相应的点,如图所示:
相应的函数值为纵坐标,描出相应的点,如图所示:
(1)请把y轴左边各点和右边各点,分别用一条光滑曲线顺次连接起来;
(2)观察图象并分析表格,回答下列问题:
①当x<0时,y随x的增大而 ;(填“增大”或“减小”)
②y=![]() 的图象是由y=﹣
的图象是由y=﹣![]() 的图象向 平移 个单位而得到;
的图象向 平移 个单位而得到;
③图象关于点 中心对称.(填点的坐标)
(3)设A(x1,y1),B(x2,y2)是函数y=![]() 的图象上的两点,且x1+x2=0,试求y1+y2+3的值.
的图象上的两点,且x1+x2=0,试求y1+y2+3的值.