题目内容
【题目】已知,如图,点 A 是直线 l 上的一点.
求作:正方形 ABCD,使得点 B 在直线 l 上.(要求保留作图痕迹,不用写作法) 请你说明,∠BAD=90°的依据是什么?
【答案】见解析.
【解析】
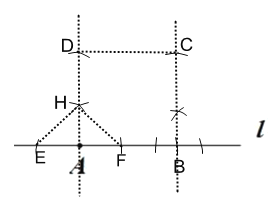
在直线l上截取AB为合适的长度,确定B点位置,然后分别过点A,点B作垂线,再分别以A,B为圆心,AB长为半径,在l的同侧截取AD=AB,BC=AB,连接CD,即可得正方形ABCD;由尺规作图的步骤结合SSS定理证明△AEH≌△AFH,即可得∠EAH=∠FAH=90°,即∠BAD=90°.
解:如图所示,正方形ABCD即为所求;
由尺规作图可知,AE=AF,EH=FH,
又∵AH=AH,
∴△AEH≌△AFH(SSS),
∴∠EAH=∠FAH,
∵∠EAH+∠FAH=180°,
∴∠EAH=∠FAH=90°,即∠BAD=90°.

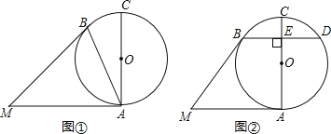
【题目】如图,AB 是⊙O 的弦,AB=5cm,点 P 是弦 AB 上的一个定点,点 C 是弧 AB 上的一 个动点,连接 CP 并延长,交⊙O 于点 D.
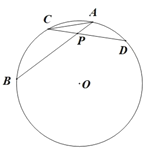
小明根据学习函数的经验,分别对 AC,PC,PD 长度之间的关系进行了探究.
下面是小明的探究过程:
(1)对于点 C 在弧 AB 上的不同位置,画图、测量,得到了线段 AC,PC,PD 的长度的 几组值,如下表:
位置 1 | 位置 2 | 位置 3 | 位置 4 | 位置 5 | 位置 6 | 位置 7 | 位置 8 | 位置 9 | |
AC/cm | 0 | 0.37 | 1.00 | 1.82 | 2.10 | 3.00 | 3.50 | 3.91 | 5.00 |
PC/cm | 1.00 | 0.81 | 0.69 | 0.75 | 1.26 | 2.11 | 2.50 | 3.00 | 4.00 |
PD/cm | 4.00 | 5.00 | 5.80 | 6.00 | 3.00 | 1.90 | 1.50 | 1.32 | 1.00 |
在 AC,PC,PD 的长度这三个量中,确定___的长度是自变量,其他两条线段的长度都是这个自变量的函数;
(2)请你在同一平面直角坐标系 xOy 中, 画(1)中所确定的两个函数的图象;

(3)结合函数图象,解决问题:
①当 PC=PD 时,AC 的长度约为 cm;
②当△APC 为等腰三角形时,PC 的长度约为 cm.