ЬтФПФкШн
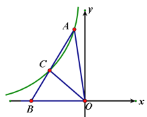
ЁОЬтФПЁПШчЭМЃЌAB ЪЧЁбO ЕФЯвЃЌAB=5cmЃЌЕу P ЪЧЯв AB ЩЯЕФвЛИіЖЈЕуЃЌЕу C ЪЧЛЁ AB ЩЯЕФвЛ ИіЖЏЕуЃЌСЌНг CP ВЂбгГЄЃЌНЛЁбO гкЕу DЃЎ
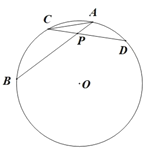
аЁУїИљОнбЇЯАКЏЪ§ЕФОбщЃЌЗжБ№Жд ACЃЌPCЃЌPD ГЄЖШжЎМфЕФЙиЯЕНјааСЫЬНОПЃЎ
ЯТУцЪЧаЁУїЕФЬНОПЙ§ГЬЃК
ЃЈ1ЃЉЖдгкЕу C дкЛЁ AB ЩЯЕФВЛЭЌЮЛжУЃЌЛЭМЁЂВтСПЃЌЕУЕНСЫЯпЖЮ ACЃЌPCЃЌPD ЕФГЄЖШЕФ МИзщжЕЃЌШчЯТБэЃК
ЮЛжУ 1 | ЮЛжУ 2 | ЮЛжУ 3 | ЮЛжУ 4 | ЮЛжУ 5 | ЮЛжУ 6 | ЮЛжУ 7 | ЮЛжУ 8 | ЮЛжУ 9 | |
AC/cm | 0 | 0.37 | 1.00 | 1.82 | 2.10 | 3.00 | 3.50 | 3.91 | 5.00 |
PC/cm | 1.00 | 0.81 | 0.69 | 0.75 | 1.26 | 2.11 | 2.50 | 3.00 | 4.00 |
PD/cm | 4.00 | 5.00 | 5.80 | 6.00 | 3.00 | 1.90 | 1.50 | 1.32 | 1.00 |
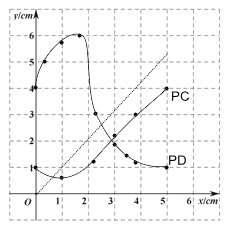
дк ACЃЌPCЃЌPD ЕФГЄЖШетШ§ИіСПжаЃЌШЗЖЈЃпЃпЃпЕФГЄЖШЪЧздБфСПЃЌЦфЫћСНЬѕЯпЖЮЕФГЄЖШЖМЪЧетИіздБфСПЕФКЏЪ§ЃЛ
ЃЈ2ЃЉЧыФудкЭЌвЛЦНУцжБНЧзјБъЯЕ xOy жаЃЌ ЛЃЈ1ЃЉжаЫљШЗЖЈЕФСНИіКЏЪ§ЕФЭМЯѓЃЛ

ЃЈ3ЃЉНсКЯКЏЪ§ЭМЯѓЃЌНтОіЮЪЬтЃК
ЂйЕБ PC=PD ЪБЃЌAC ЕФГЄЖШдМЮЊ cmЃЛ
ЂкЕБЁїAPC ЮЊЕШбќШ§НЧаЮЪБЃЌPC ЕФГЄЖШдМЮЊ cm.
ЁОД№АИЁПЃЈ1ЃЉACЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉЂй2.9ЃЌЂк0.69cmЛђ1cmЛђ0.8cmЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнБфСПКЭКЏЪ§ЕФЖЈвхНсКЯЬтвтЗжЮіМДПЩЃЛ
ЃЈ2ЃЉИљОнБэжаЪ§ОнУшГіВПЗжЕуЃЌШЛКѓСЌЯпМДПЩЃЛ
ЃЈ3ЃЉЂйСНКЏЪ§ЭМЯѓНЛЕуДІЕФКсзјБъОЭЪЧPC=PDЪБACЕФГЄЖШЃЛ
ЂкЧѓГіAPЃН1cmЃЌШЛКѓЗжAPЃНACЃЌAPЃНPCКЭACЃНPCШ§жжЧщПіЃЌЗжБ№ЧѓНтМДПЩЃЎ
НтЃКЃЈ1ЃЉгЩгкPCКЭPDЫцзХACЕФБфЛЏЖјБфЛЏЃЌ
ЁрШЗЖЈACЕФГЄЖШЪЧздБфСПЃЌЦфЫћСНЬѕЯпЖЮЕФГЄЖШЖМЪЧетИіздБфСПЕФКЏЪ§ЃЌ
ЙЪД№АИЮЊЃКACЃЛ
ЃЈ2ЃЉКЏЪ§ЭМЯѓШчЭМЫљЪОЃК
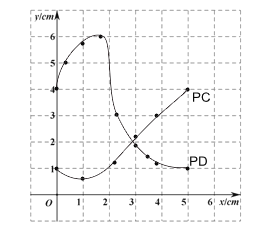
ЃЈ3ЃЉЂйгЩКЏЪ§ЭМЯѓЕУЃКЕБPC=PDЪБЃЌACЕФГЄЖШдМЮЊ2.9cmЃЛ
ЂкЁпЕБACЃН0ЪБЃЌЕуAКЭЕуCжиКЯЃЌДЫЪБPCЃН1cmЃЌ
ЁрAPЃН1cmЃЌ
ЕБAPЃНACЃН1cmЪБЃЌгЩБэИёЕУЃЌPCЃН0.69cmЃЌ
ЕБAPЃНPCЃН1cmЪБЃЌдђPCЃН1cmЃЌ
ЕБACЃНPCЪБЃЌШчЭМЃЌгЩКЏЪ§ЭМЯѓЕУЃЌPCЁж0.8cmЃЌ
злЩЯЫљЪіЃЌPCЕФГЄЖШдМЮЊ0.69cmЛђ1cmЛђ0.8cmЃЎ

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ