题目内容
【题目】已知⊙![]() 中,
中,![]() 为直径,
为直径,![]() 、
、![]() 分别切⊙
分别切⊙![]() 于点
于点![]() 、
、![]() .
.
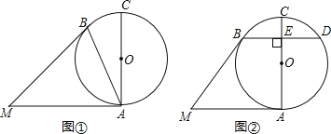
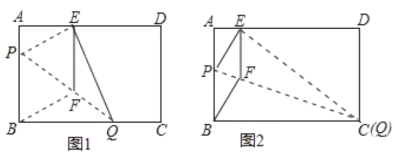
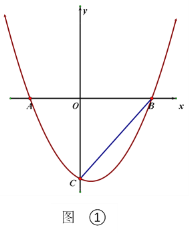
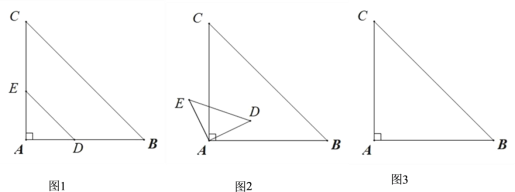
(1)如图①,若![]() ,求
,求![]() 的大小;
的大小;
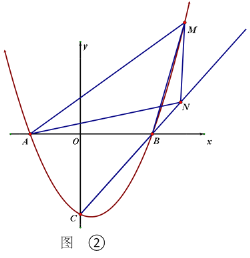
(2)如图②,过点![]() 作
作![]() ∥
∥![]() ,交
,交![]() 于点
于点![]() ,交⊙
,交⊙![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的大小.
的大小.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根据切线性质求出∠OBM=∠OAM=90°,根据圆周角定理求出∠COB,求出∠BOA,即可求出答案;
(2)连接AB、AD,得出平行四边形,推出MB=AD,推出AB=AD,求出等边三角形AMB,即可得出答案.
(1)连接OB,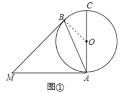
∵MA、MB分别切⊙O于A.B,
∴∠OBM=∠OAM=90°,
∵弧BC对的圆周角是∠BAC,圆心角是∠BOC,∠BAC=25°,
∴∠BOC=2∠BAC=50°,
∴∠BOA=180°50°=130°,
∴∠AMB=360°90°90°130°=50°.
(2)连接AD,AB,
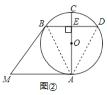
∵BD∥AM,DB=AM,
∴四边形BMAD是平行四边形,
∴BM=AD,
∵MA切⊙O于A,
∴AC⊥AM,
∵BD∥AM,
∴BD⊥AC,
∵AC过O,
∴BE=DE,
∴AB=AD=BM,
∵MA、MB分别切⊙O于A.B,
∴MA=MB,
∴BM=MA=AB,
∴△BMA是等边三角形,
∴∠AMB=60°.

 通城学典默写能手系列答案
通城学典默写能手系列答案【题目】某服装商城每月付给销售人员的工资有两种方案,已知计件工资与销售件数成正比例.有甲、乙两种品牌服装销售人员,如果销售量为![]() 件,销售甲品牌服装的工资是
件,销售甲品牌服装的工资是![]() (元),销售乙品牌服装的工资是
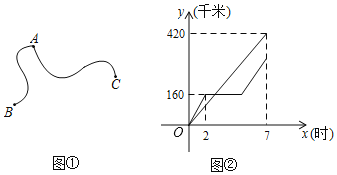
(元),销售乙品牌服装的工资是![]() (元),销售件数与工资之间的关系如图所示,已知销售甲品牌服装的每月底薪是800元,每销售一件甲品牌服装每件所得的提成比乙高2元,不管销售那种品牌服装,销售量超过80件(不含80件),
(元),销售件数与工资之间的关系如图所示,已知销售甲品牌服装的每月底薪是800元,每销售一件甲品牌服装每件所得的提成比乙高2元,不管销售那种品牌服装,销售量超过80件(不含80件),
则每件多提成6元.下表是半年内甲乙两产品的销售量:
时间 | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 |
甲品牌服装销量 | 90 | 120 | 130 | 80 | 100 | 110 |
乙品牌服装销量 | 70 | 60 | 90 | 80 | 110 | 100 |
(1)现从半年内随机抽取1个月,求这一月乙品牌服装销售量超过80件(不含80)的概率;
(2)根据图中信息,求销售乙品牌服装的底薪是多少元?
(3)小明拟销售甲、乙两种品牌服装,如果仅从工资收人的角度考虑,请利用所学的统计知识帮他选择,并说明理由.