题目内容
【题目】“壮丽70载,奋进新时代”.值伟大祖国70华诞之际,某网店特别推出甲、乙两种纪念文化衫,已知甲种纪念文化衫的售价比乙种纪念文化衫多15元,广益中学陈老师从该网店购买了2件甲种纪念文化衫和3件乙种纪念文化衫,共花费255元.
(1)该网店甲、乙两种纪念文化衫每件的售价各是多少元?
(2)根据消费者需求,该网店决定用不超过8780元购进甲、乙两种纪念文化衫共200件,且甲种纪念文化衫的数量大于乙种纪念文化衫数量的![]() ,已知甲种纪念文化衫每件的进价为50元,乙种纪念文化衫每件的进价为40元.
,已知甲种纪念文化衫每件的进价为50元,乙种纪念文化衫每件的进价为40元.
①若设购进甲种纪念文化衫m件,则该网店有哪几种进货方案?
②若所购进纪念文化衫均可全部售出,请求出网店所获利润W(元)与甲种纪念文化衫进货量m(件)之间的函数关系式,并说明当m为何值时所获利润最大?最大利润是多少?
【答案】(1)甲种纪念文化衫每件的售价是60元,乙种纪念文化衫每件的售价是45元;(2)①进货方案有三种,分别为:方案一:购进甲种纪念文化衫76件,则乙种纪念文化衫为124件;方案二:购进甲种纪念文化衫77件,则乙种纪念文化衫为123件;方案三:购进甲种纪念文化衫78件,则乙种纪念文化衫为122件;②W=5m+1000,当m=78时,所获利润最大,最大利润为1390元.
【解析】
(1)设甲种纪念文化衫每件的售价是x元,乙种纪念文化衫每件的售价是y元,由题意,列二元一次方程组,求解即可;(2)①若购进甲种纪念文化衫m件,则乙种纪念文化衫为(200m)件,由题意得一元一次不等式组,求解,并根据m为整数,可求得m的值,即可得进货方案;②用含m的式子表示出W,根据一次函数的性质可得答案.
解:(1)设甲种纪念文化衫每件的售价是x元,乙种纪念文化衫每件的售价是y元,由题意得:
![]()
解得:![]()
答:甲种纪念文化衫每件的售价是60元,乙种纪念文化衫每件的售价是45元.
(2)①若购进甲种纪念文化衫m件,则乙种纪念文化衫为(200﹣m)件,
由题意得:
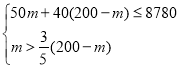
解得:75<m≤78
∵m为整数
∴m的值为:76,77,78.
进货方案有三种,分别为:
方案一:购进甲种纪念文化衫76件,则乙种纪念文化衫为124件;
方案二:购进甲种纪念文化衫77件,则乙种纪念文化衫为123件;
方案三:购进甲种纪念文化衫78件,则乙种纪念文化衫为122件.
②由题意得:
W=(60﹣50)m+(45﹣40)(200﹣m)=5m+1000
∵5>0
∴W随m的增大而增大,且75<m≤78
∴当m=78时,W最大,W的最大值为:5×78+1000=1390元.
答:②当m=78时,所获利润最大,最大利润为1390元.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案