题目内容
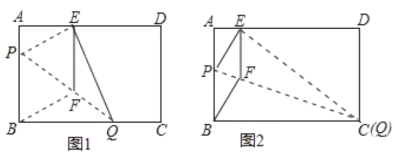
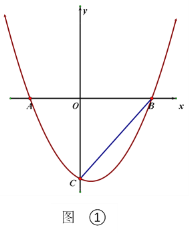
【题目】如图1所示的是一种折叠门,已知门框的宽度AD=2米,两扇门的大小相同(即AB=CD),且AB+CD=AD,现将右边的门CDD1C1绕门轴DD1向外面旋转67°(如图2).
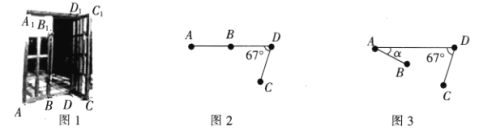
(1)求点C到AD的距离.
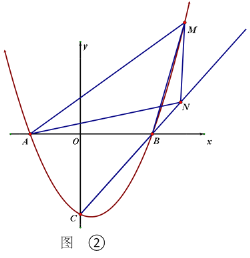
(2)将左边的门ABB1A1绕门轴AA1向外面旋转,设旋转角为α(如图3),问α为多少时,点B,C之间的距离最短?(参考数据:sin67°≈0.92,cos67°≈0.39,tan29.6°≈0.57,tan19.6°≈0.36,sin29.6°≈0.49)
【答案】(1)点C到AD的距离约为0.92米;(2)29.6°
【解析】
(1)过点C作CH⊥AD于点H,然后利用CH=CD·sin67°即可求解;
(2)当A、B、C三点共线时,点B,C之间的距离最短,过点C作CH⊥AD于点H,连接BC,先求出DH的长度,进而求出AH的长度,最后利用![]() 求出
求出![]() ,则角度可求.
,则角度可求.
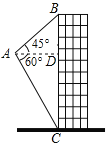
解:(1)如图1,过点C作CH⊥AD于点H.
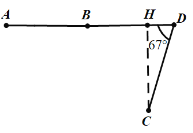
由题意得∠D=67°,CD=![]() AD=1米,
AD=1米,
∴CH=CD·sin67°≈![]() 米.
米.
答:点C到AD的距离约为0.92米.
(2)当A、B、C三点共线时,点B,C之间的距离最短.
如图2,过点C作CH⊥AD于点H,连接BC.
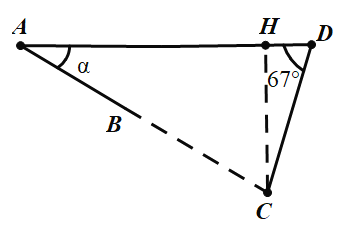
DH=CD·cos67°≈0.39米,
∴AH=AD-DH=2-0.39=1.61米.
由(1)知CH≈0.92米,
在Rt![]() ACH中,
ACH中, ![]() =
=![]() ≈0.57,
≈0.57,
∴![]() .
.
答:当![]() 为29.6°时,点B,C之间的距离最短.
为29.6°时,点B,C之间的距离最短.

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案【题目】某服装商城每月付给销售人员的工资有两种方案,已知计件工资与销售件数成正比例.有甲、乙两种品牌服装销售人员,如果销售量为![]() 件,销售甲品牌服装的工资是
件,销售甲品牌服装的工资是![]() (元),销售乙品牌服装的工资是
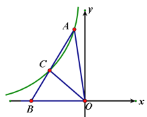
(元),销售乙品牌服装的工资是![]() (元),销售件数与工资之间的关系如图所示,已知销售甲品牌服装的每月底薪是800元,每销售一件甲品牌服装每件所得的提成比乙高2元,不管销售那种品牌服装,销售量超过80件(不含80件),
(元),销售件数与工资之间的关系如图所示,已知销售甲品牌服装的每月底薪是800元,每销售一件甲品牌服装每件所得的提成比乙高2元,不管销售那种品牌服装,销售量超过80件(不含80件),
则每件多提成6元.下表是半年内甲乙两产品的销售量:
时间 | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 |
甲品牌服装销量 | 90 | 120 | 130 | 80 | 100 | 110 |
乙品牌服装销量 | 70 | 60 | 90 | 80 | 110 | 100 |
(1)现从半年内随机抽取1个月,求这一月乙品牌服装销售量超过80件(不含80)的概率;
(2)根据图中信息,求销售乙品牌服装的底薪是多少元?
(3)小明拟销售甲、乙两种品牌服装,如果仅从工资收人的角度考虑,请利用所学的统计知识帮他选择,并说明理由.