Question

如图，已知⊙O和⊙O′相交于A、B两点，过点A作⊙O′的切线交⊙O于点C，过点B作两圆的割线分别交⊙O、⊙O′于E、F，EF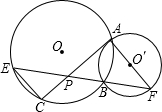与AC相交于点P．
（1）求证：PA•PE=PC•PF；
（2）求证：

PE2

PC2

=

PF

PB

；
（3）当⊙O与⊙O′为等圆时，且PC：CE：EP=3：4：5时，求△PEC与△FAP的面积的比值．

Answer 1

（1）证明：连接AB，
∵CA切⊙O'于A，
∴∠CAB=∠F．
∵∠CAB=∠E，
∴∠E=∠F．
∴AF∥CE．
∴

PE

PF

=

PC

PA

．
∴PA•PE=PC•PF．

（2）证明：∵

PE

PF

=

PC

PA

，
∴

PE2

PF2

=

PC2

PA2

．
∴

PE2

PC2

=

PF2

PA2

．
再根据切割线定理，得PA²=PB•PF，
∴

PE2

PC2

=

PF

PB

．

（3）连接AE，由（1）知△PEC∽△PFA，
而PC：CE：EP=3：4：5，
∴PA：FA：PF=3：4：5．
设PC=3x，CE=4x，EP=5x，PA=3y，FA=4y，PF=5y，
∴EP²=PC²+CE²，PF²=PA²+FA²．
∴∠C=∠CAF=90°．
∴AE为⊙O的直径，AF为⊙O'的直径．
∵⊙O与⊙O'等圆，
∴AE=AF=4y．
∵AC²+CE²=AE²
∴（3x+3y）²+（4x）²=（4y）²即25x²+18xy-7y²=0，
∴（25x-7y）（x+y）=0，
∴

x

y

=

7

25

．
∴S△ECP：S△FAP=

x2

y2

=

49

625

．