Question

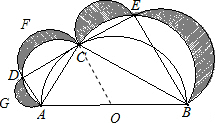
如图，以AB为直径作半圆与直角梯形ABED另一腰DE相切于C点，再分别以AC、BC、
AD、CD、CE、BE为直径作半圆．若AC=3，BC=4，则图中阴影部分的面积和为______．

Answer 1

取AB的中点O，连接OC，
∵AB是⊙O的直径，
∴∠ACB=90°，
∵AC=3，BC=4，
∴AB=

AC2+BC2

=

32+42

=5，
∵DE是⊙O的切线，
∴OC⊥DE，
∵梯形ABED是直角梯形，
∴∠ADC=∠BEC=90°，
∴OC是梯形ABED的中位线，
∴CD=CE，

AD+BE

2

=OC，
∴OA=OC=

AB

2

=

5

2

，
∵梯形ABED是直角梯形，
∴∠ADC=∠BEC=90°，
∴AC²-AD²=BC²-BE²，即3²-（2OC-BE）²=4²-BE²，即3²-（5-BE）²=4²-BE²，解得BE=3.2，
∴CD=CE=

BC2-BE2

=

42-3.22

=

12

5

，
∴DE=2CE=2×

12

5

=

24

5

，
∵△ACD是直角三角形，
∴AC2=AD²+CD²，
∴（

AC

2

）²=（

CD

2

）²+（

AD

2

）²，
即以AC为半径的圆的半圆的面积等于以CD为半径的半圆与以AD为半径的半圆面积的和，
∴以CD为半径的半圆阴影部分与以AD为半径的半圆阴影部分面积的和等于Rt△ACD的面积，
同理可得，以BE为半径的半圆阴影部分与以CE为半径的半圆阴影部分面积的和等于Rt△CBE的面积，
∴S_阴影=S_梯形ABED-S_△ABC=

(AD+BE)×DE

2

-

1

2

AC×BC=OC×DE-

1

2

AC×BC=2.5×

24

5

-

1

2

×3×4=6．
故答案为：6．