题目内容
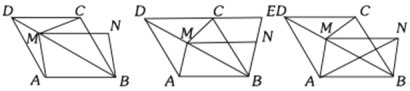
【题目】如图1，在菱形ABCD中，AB=
，∠BCD=120°，M为对角线BD上一点（M不与点B、D重合），过点MN∥CD，使得MN=CD，连接CM、AM、BN.
（1）当∠DCM=30°时，求DM的长度；
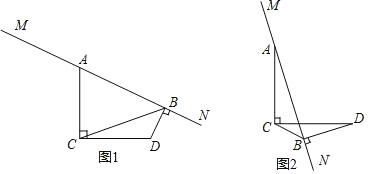
（2）如图2，延长BN、DC交于点E，求证：AM·DE=BE·CD；
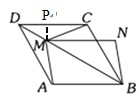
（3）如图3，连接AN，则AM+AN的最小值是 .
【答案】（1）1;（2）见解析;（3）当BN⊥CD时有最小值3.
【解析】
（1）过点M作MP⊥CD于点P，根据菱形的性质求∠DCM=30°，进而可知∠CDM=∠DCM，△DMC是等腰三角形，再利用等腰三线合一，求得
，进而可得DM值.
（2）先根据已知条件证得四边形ABCD是平行四边形，求得MN=CD，NB=AM，利用平分线所分线段对应成比例得到
，再进行等量代换即可答案.
（3）根据题意可知当AM⊥MN时，AM+AN的最小值，利用特殊三角函数值求得此时AM、MN的值即可.
（1）
过点M作MP⊥CD于点P
∵四边形ABCD是菱形, AB=
∴CD=AB=BC=
∴∠CDB=
∵∠DCM=30°
∴∠CDM=∠DCM
∴△DMC是等腰三角形
∵MP⊥CD
∴
∴DM=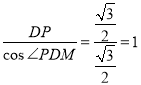
（2）∵四边形ABCD 是菱形
∴CD=AB，AB∥CD
∵MN=CD，MN∥CD
∴MN=AB，MN∥AB
∴四边形ABMN是平行四边形
∴NB=AM
∵MN∥CD
∴
∵MN=CD，NB=AM
∴
即AM·DE=BE·CD
（3）由（2）可知MN=AB=,那么根据题意当AM⊥MN时，AM+AN最短.
∵∠CDB=
（已求），DC∥AB
∴∠MBA=∠CDB=
∵AM⊥MN,MN∥AB
∴∠MAB=
∵AB=
∴AM=1
∴在Rt△AMN中，利用勾股定理得
则AM+AN=1+2=3
∴当BN⊥CD时，AM+AN有最小值3.
【题目】二次函数y＝ax2＋bx＋c（a，b，c 为常数，且a≠0）的图像上部分点的横坐标x和纵
坐标y的对应值如下表
x | … | －1 | 0 | 1 | 2 | 3 | … |
y | … | －3 | －3 | －1 | 3 | 9 | … |
关于x的方程ax2＋bx＋c＝0一个负数解x1满足k＜x1＜k+1（k为整数），则k＝________．
