题目内容
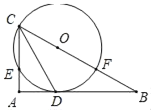
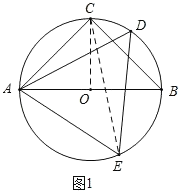
【题目】已知:△ABC是⊙O的内接三角形,AB为直径,AC=BC,D、E是⊙O上两点,连接AD、DE、AE.

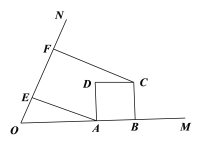
(1)如图1,求证:∠AED﹣∠CAD=45°;
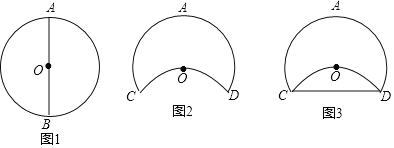
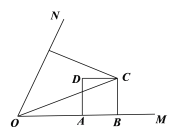
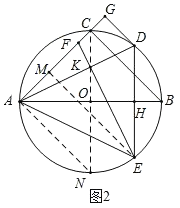
(2)如图2,若DE⊥AB于点H,过点D作DG⊥AC于点G,过点E作EK⊥AD于点K,交AC于点F,求证:AF=2DG;
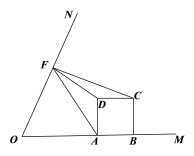
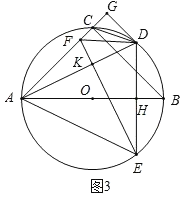
(3)如图3,在(2)的条件下,连接DF、CD,若∠CDF=∠GAD,DK=3,求⊙O的半径.
【答案】(1)见解析;(2)见解析;(3)⊙O的半径为![]()
【解析】
(1)连接CO,CE,证∠B=45°,可依次推出∠AED﹣∠CAD=∠AED﹣∠CED=∠AEC=![]() ∠COA=45°,即可写出结论;
∠COA=45°,即可写出结论;
(2)连接CO并延长,交⊙O于点N,连接AN,过点E作EM⊥AC于M,证△ADG≌△EAM,△ADG≌△EFM,即可推出AF=2DG;
(3)证△FCD∽△DCA,推出△GFD为等腰直角三角形,设GF=GD=a,分别用含a的代数式表示DF,AF,FK,在Rt△FKD中,即可求出a的值,再利用△FCD∽△DCA,求出FC的值,即可求得AC的值,进一步求出AB的值,即可求得半径.
(1)证明:如图1,连接CO,CE,
∵AB是直径,
∴∠ACB=90°,
∵AC=BC,
∴∠B=∠CAB=45°,
∴∠COA=2∠B=90°,
∵![]() ,
,
∴∠CAD=∠CED,
∴∠AED﹣∠CAD=∠AED﹣∠CED=∠AEC=![]() ∠COA=45°,
∠COA=45°,
即∠AED﹣∠CAD=45°;
(2)如图2,连接CO并延长,交⊙O于点N,连接AN,过点E作EM⊥AC于M,
则∠CAN=90°,
∵AC=BC,AO=BO,
∴CN⊥AB,
∴AB垂直平分CN,
∴AN=AC,
∴∠NAB=∠CAB,
∵AB垂直平分DE,
∴AD=AE,
∴∠DAB=∠EAB,
∴∠NAB﹣∠EAB=∠CAB﹣∠DAB,
即∠GAD=∠NAE,
∵∠CAN=∠CME=90°,
∴AN∥EB,
∴∠NAE=∠MEA,
∴∠GAD=∠MEA,
又∵∠G=∠AME=90°,AD=EA,
∴△ADG≌△EAM(AAS),
∴AG=EM,AM=DG,
又∵∠MEF+∠MFE=90°,∠MFE+∠GAD=90°,
∴∠MEF=∠GAD,
又∵∠G=∠FME=90°,
∴△ADG≌△EFM(ASA),
∴DG=MF,
∵DG=AM,
∴AF=AM+MF=2DG;
(3)∵∠CDF=∠GAD,∠FCD=∠DCA,
∴△FCD∽△DCA,
∴∠CFD=∠CDA=∠CBA,
∵AC=BC,AB为直径,
∴△ABC为等腰直角三角形,
∴∠CFD=∠CDA=∠CBA=45°,
∴△GFD为等腰直角三角形,
设GF=GD=a,则FD=![]() a,AF=2a,
a,AF=2a,
∴![]()
∵∠FAK=∠DAG,∠AKF=∠G=90°,
∴△AFK∽△ADG,
∴![]() ,
,
在Rt△AFK中,
设FK=x,则AK=3x,
∵FK2+AK2=AF2,
∴x2+(3x)2=(2a)2,
解得,x=![]() a(取正值),
a(取正值),
∴FK=![]() a,
a,
在Rt△FKD中,FK2+DK2=FD2,
∴(![]() a)2+32=(
a)2+32=(![]() a)2,
a)2,
解得,a=![]() (取正值),
(取正值),
∴GF=GD=![]() ,AF=
,AF=![]() ,
,
∵△FCD∽△DCA,
∴![]()
∴CD2=CAFC,
∵CD2=CG2+GD2,
∴CG2+GD2=CAFC,
设FC=n,
则![]()
解得,n=![]() ,
,
∴AC=AF+CF=![]()
∴AB=![]() AC=
AC=![]() ,
,
⊙O的半径为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
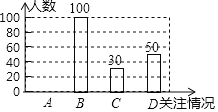
小学生10分钟应用题系列答案【题目】2019年2月18日,“时代楷模”、伏牛山里的好教师﹣﹣张玉滚当选“感动中国”2018年度人物,在中原大地引起强烈反响.为了解学生对张玉滚事迹的知晓情况,某数学课外兴趣小组在本校学生中开展了专题调查活动,随机抽取了部分学生进行问卷调查,根据学生的答题情况,将结果分为A,B,C,D四类,将调查的数据整理后绘制成如下统计表及条形统计图(均不完整):
关注情况 | 频数 | 频率 |
A.非常了解 | m | 0.1 |
B.比较了解 | 100 | 0.5 |
C.基本了解 | 30 | n |
D.不太了解 | 50 | 0.25 |
根据以上信息解答下列问题:
(1)在这次抽样调查中,一共抽查了 名学生;
(2)统计表中,m= ,n= ;
(3)请把条形统计图补充完整;
(4)该校共有学生1500名,请你估算该校学生中对张玉滚事迹“非常了解“和“比较了解”的学生共有多少名.