Question

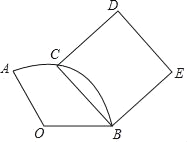
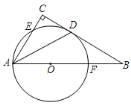
【题目】已知AC＝DC，AC⊥DC，直线MN经过点A，作DB⊥MN，垂足为B，连接CB．

（1）直接写出∠D与∠MAC之间的数量关系；

（2）①如图1，猜想AB，BD与BC之间的数量关系，并说明理由；

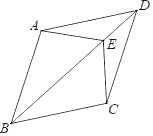
②如图2，直接写出AB，BD与BC之间的数量关系；

（3）在MN绕点A旋转的过程中，当∠BCD＝30°，BD＝时，直接写出BC的值．

Answer 1

【答案】（1）相等或互补；（2）①BD+AB＝BC；②AB﹣BD＝BC；（3）BC＝ 或.

【解析】

（1）分为点C，D在直线MN同侧和点C，D在直线MN两侧,两种情况讨论即可解题,

（2）①作辅助线,证明△BCD≌△FCA，得BC＝FC，∠BCD＝∠FCA,∠FCB＝90°,即△BFC是等腰直角三角形,即可解题, ②在射线AM上截取AF＝BD，连接CF，证明△BCD≌△FCA，得△BFC是等腰直角三角形,即可解题,

（3）分为当点C，D在直线MN同侧，当点C，D在直线MN两侧，两种情况解题即可,见详解.

解：（1）相等或互补；

理由：当点C，D在直线MN同侧时，如图1，

∵AC⊥CD，BD⊥MN，

∴∠ACD＝∠BDC＝90°，

在四边形ABDC中，∠BAD+∠D＝360°﹣∠ACD﹣∠BDC＝180°，

∵∠BAC+∠CAM＝180°，

∴∠CAM＝∠D；

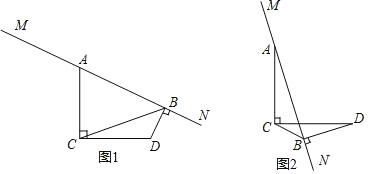
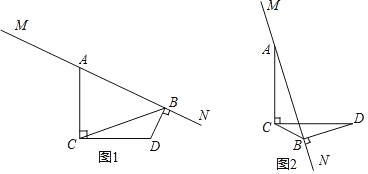
当点C，D在直线MN两侧时，如图2，

∵∠ACD＝∠ABD＝90°，∠AEC＝∠BED，

∴∠CAB＝∠D，

∵∠CAB+∠CAM＝180°，

∴∠CAM+∠D＝180°，

即：∠D与∠MAC之间的数量是相等或互补；

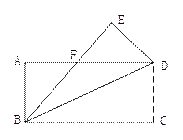
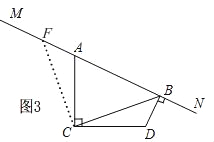
（2）①猜想：BD+AB＝BC

如图3，在射线AM上截取AF＝BD，连接CF．

又∵∠D＝∠FAC，CD＝AC

∴△BCD≌△FCA，

∴BC＝FC，∠BCD＝∠FCA

∵AC⊥CD

∴∠ACD＝90°

即∠ACB+∠BCD＝90°

∴∠ACB+∠FCA＝90°

即∠FCB＝90°

∴BF＝

∵AF+AB＝BF＝

∴BD+AB＝；

②如图2，在射线AM上截取AF＝BD，连接CF，

又∵∠D＝∠FAC，CD＝AC

∴△BCD≌△FCA，

∴BC＝FC，∠BCD＝∠FCA

∵AC⊥CD

∴∠ACD＝90°

即∠ACB+∠BCD＝90°

∴∠ACB+∠FCA＝90°

即∠FCB＝90°

∴BF＝

∵AB﹣AF＝BF＝

∴AB﹣BD＝；

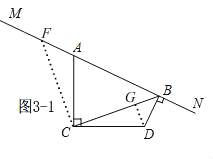
（3）①当点C，D在直线MN同侧时，如图3﹣1，

由（2）①知，△ACF≌△DCB，

∴CF＝BC，∠ACF＝∠ACD＝90°，

∴∠ABC＝45°，

∵∠ABD＝90°，

∴∠CBD＝45°，

过点D作DG⊥BC于G，

在Rt△BDG中，∠CBD＝45°，BD＝，

∴DG＝BG＝1，

在Rt△CGD中，∠BCD＝30°，

∴CG＝DG＝，

∴BC＝CG+BG＝+1，

②当点C，D在直线MN两侧时，如图2﹣1，

过点D作DG⊥CB交CB的延长线于G，

同①的方法得，BG＝1，CG＝，

∴BC＝CG﹣BG＝﹣1

即：BC＝ 或，