题目内容
如图,△ABC是边长为2的等边三角形,将△ABC沿射线BC向右平移得到△DCE,连接AD、BD,下列结论错误的是( )
A.AD∥BC B.AC⊥BD
C.四边形ABCD面积为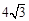 D.四边形ABED是等腰梯形
D.四边形ABED是等腰梯形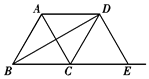
A.AD∥BC B.AC⊥BD
C.四边形ABCD面积为
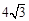 D.四边形ABED是等腰梯形
D.四边形ABED是等腰梯形
C
A、经过平移,对应点所连的线段平行且相等,对应线段平行且相等,AD∥BC,故正确;
B、由菱形的性质知,对角线互相垂直,所以有AC⊥BD,故正确;
C、∵△ABC≌△CED,∴AB=BC=CE=DE=CD,∠ACB=∠ECD=60°,
∴∠ACD=180°-∠ACB-∠ECD=60°,∴△ACD也是等边三角形,有AD=AB=BC=CD,
∴四边形ADCB是菱形,∴SABCD=2S△ABC=2×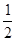 ×AB×BC×sin60°=2
×AB×BC×sin60°=2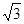 ,故错误;
,故错误;
D、∵AD∥BE,AB=DE,∴四边形ABED是等腰梯形,故正确.故选C.
B、由菱形的性质知,对角线互相垂直,所以有AC⊥BD,故正确;
C、∵△ABC≌△CED,∴AB=BC=CE=DE=CD,∠ACB=∠ECD=60°,
∴∠ACD=180°-∠ACB-∠ECD=60°,∴△ACD也是等边三角形,有AD=AB=BC=CD,
∴四边形ADCB是菱形,∴SABCD=2S△ABC=2×
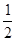 ×AB×BC×sin60°=2
×AB×BC×sin60°=2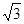 ,故错误;
,故错误;D、∵AD∥BE,AB=DE,∴四边形ABED是等腰梯形,故正确.故选C.

练习册系列答案
相关题目
 ,
, ,圆A与圆C交于B、D两点),连结AB、BC、CD、DA.若能作出满足要求的四边形ABCD,则
,圆A与圆C交于B、D两点),连结AB、BC、CD、DA.若能作出满足要求的四边形ABCD,则 应满足什么条件?
应满足什么条件? ,求四边形ABCD的面积.
,求四边形ABCD的面积. 为
为 边的中点,延长
边的中点,延长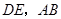 相交于点
相交于点 .
. .
.