题目内容
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延
长EF交边BC于点G,连结AG、CF.下列结论:
①△ABG≌△AFG;②BG=GC;③AG∥CF; ④S△FGC=3.
其中正确结论的个数是

长EF交边BC于点G,连结AG、CF.下列结论:
①△ABG≌△AFG;②BG=GC;③AG∥CF; ④S△FGC=3.
其中正确结论的个数是
| A.1个 | B.2个 | C.3个 | D.4个 |

C
对折可得:DE="EF" ,AF="AD" ,AF⊥EF , △ADE≌△AFE
①在Rt△ABG与Rt△AFG中,AB="AF" ,AG=AG,所以,Rt△ABG≌Rt△AFG①正确。②Rt△ABG≌Rt△AFG可得:BG="FG" ,∠AGB=∠AGF设BG="x" 则,CG="BC-BG" = 6-xGE=GF+EF=BG+DE=x+2在Rt△ECG中,有CG^2+CE^2="EG^2CG=6-x" , CE="4" ,EG=x+2可得:(6-x)^2 + 4^2 = (x+2)^2解得:x=3所以,BG=GF=CG=3 结论②正确。③因为,CG=GF所以,∠CFG = ∠FCG因为,∠BGF=∠CFG+∠FCG(三角形的外角等于不相邻的两个内角和)又∠BGF=∠AGB+∠AGF可得:∠CFG+∠FCG = ∠AGB+∠AGF因为,∠AGB=∠AGF,∠CFG = ∠FCG所以,2∠AGB=2∠FCG即,∠AGB=∠FCG所以,AG//CF结论③正确。
④∵AB=AD=AF,AG=AG,∠B=∠AFG=90°,∴△ABG≌△AFG;∴BG="FG∵EF=DE=" CD=2,设BG=FG=x,则CG=6-x.
在直角△ECG中,根据勾股定理,得(6-x)2+42=(x+2)2,解得x=3.所以BG=3=6-3=GC过F作FH⊥DC,∵BC⊥DH,∴FH∥GC,∴△EFH∽△EGC,∴FH/GC="EF/EG" ,EF=DE=2,GF=3,∴EG=5,∴FH/GC="EF/EG=2/5" ,∴S△FCG="S△GCE-S△FEC=" 1/2×3×4-1/2 ×4×(2/5 ×3)=18/5结论④错误。故选C
①在Rt△ABG与Rt△AFG中,AB="AF" ,AG=AG,所以,Rt△ABG≌Rt△AFG①正确。②Rt△ABG≌Rt△AFG可得:BG="FG" ,∠AGB=∠AGF设BG="x" 则,CG="BC-BG" = 6-xGE=GF+EF=BG+DE=x+2在Rt△ECG中,有CG^2+CE^2="EG^2CG=6-x" , CE="4" ,EG=x+2可得:(6-x)^2 + 4^2 = (x+2)^2解得:x=3所以,BG=GF=CG=3 结论②正确。③因为,CG=GF所以,∠CFG = ∠FCG因为,∠BGF=∠CFG+∠FCG(三角形的外角等于不相邻的两个内角和)又∠BGF=∠AGB+∠AGF可得:∠CFG+∠FCG = ∠AGB+∠AGF因为,∠AGB=∠AGF,∠CFG = ∠FCG所以,2∠AGB=2∠FCG即,∠AGB=∠FCG所以,AG//CF结论③正确。
④∵AB=AD=AF,AG=AG,∠B=∠AFG=90°,∴△ABG≌△AFG;∴BG="FG∵EF=DE=" CD=2,设BG=FG=x,则CG=6-x.
在直角△ECG中,根据勾股定理,得(6-x)2+42=(x+2)2,解得x=3.所以BG=3=6-3=GC过F作FH⊥DC,∵BC⊥DH,∴FH∥GC,∴△EFH∽△EGC,∴FH/GC="EF/EG" ,EF=DE=2,GF=3,∴EG=5,∴FH/GC="EF/EG=2/5" ,∴S△FCG="S△GCE-S△FEC=" 1/2×3×4-1/2 ×4×(2/5 ×3)=18/5结论④错误。故选C

练习册系列答案
相关题目

 中,若
中,若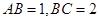 ,则平行四边形
,则平行四边形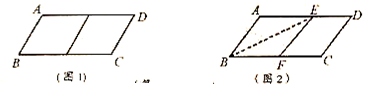
 折叠(点
折叠(点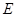 在
在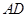 上)使点
上)使点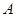 落在
落在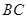 边上的点
边上的点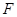 ,得到四边形
,得到四边形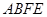 ,请证明四边形
,请证明四边形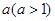 裁剪线的示意图,并在图形下方写出
裁剪线的示意图,并在图形下方写出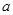 的值;
的值;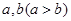 ,满足
,满足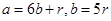 ,请写出平行四边形
,请写出平行四边形
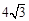 D.四边形ABED是等腰梯形
D.四边形ABED是等腰梯形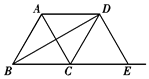
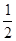 BF; ②∠CHF=45°; ③GH=
BF; ②∠CHF=45°; ③GH=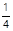 BC;④DH2=HE·HB
BC;④DH2=HE·HB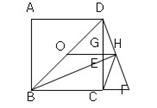
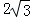 ,2)、C(0,4),过点C向右作平行于x轴的射线,点P是射线上的动点,连接AP,以AP为边在其左侧作等边△APQ,连接PB、BA.若四边形ABPQ为梯形,则:
,2)、C(0,4),过点C向右作平行于x轴的射线,点P是射线上的动点,连接AP,以AP为边在其左侧作等边△APQ,连接PB、BA.若四边形ABPQ为梯形,则: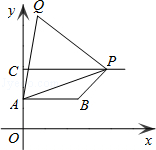
 ABCD中,BE平分∠ABC并与AD,CD的延长线交于点E,F,AB=3,BC=5,则DF= ▲ .
ABCD中,BE平分∠ABC并与AD,CD的延长线交于点E,F,AB=3,BC=5,则DF= ▲ .