题目内容
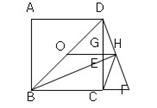
如图,△ABC中,∠B=90°,AB=6,BC=8,将△ABC沿DE折叠,使点C落在AB边上的C′处,并且C′D∥BC,则CD的长是 ▲ 

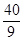
设CD=x,
根据C′D∥BC,且有C′D=EC,
可得四边形C′DCE是菱形;
即Rt△BC′E中,
AC=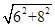 =10,
=10,
BE/8 =C′E/10 ="CD/10" ="X/10" ,
EB=4/5x;
故可得BC=x+4/5x=8;
解得x="40/9" .
根据C′D∥BC,且有C′D=EC,
可得四边形C′DCE是菱形;
即Rt△BC′E中,
AC=
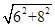 =10,
=10,BE/8 =C′E/10 ="CD/10" ="X/10" ,
EB=4/5x;
故可得BC=x+4/5x=8;
解得x="40/9" .

练习册系列答案
相关题目
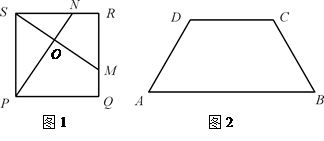
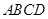 中,若
中,若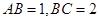 ,则平行四边形
,则平行四边形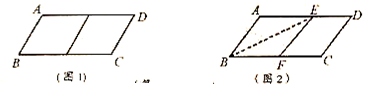
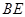 折叠(点
折叠(点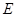 在
在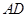 上)使点
上)使点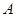 落在
落在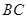 边上的点
边上的点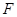 ,得到四边形
,得到四边形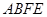 ,请证明四边形
,请证明四边形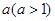 裁剪线的示意图,并在图形下方写出
裁剪线的示意图,并在图形下方写出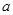 的值;
的值;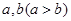 ,满足
,满足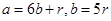 ,请写出平行四边形
,请写出平行四边形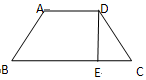

 D.四边形ABED是等腰梯形
D.四边形ABED是等腰梯形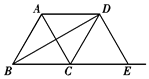
 BF; ②∠CHF=45°; ③GH=
BF; ②∠CHF=45°; ③GH= BC;④DH2=HE·HB
BC;④DH2=HE·HB