Question

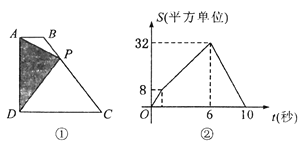
【题目】如图①，四边形中，，，从点出发，以每秒2个单位长度的速度，按的顺序在边上匀速运动，设点的运动时间为秒，的面积为，关于的函数图像如图②所示，当运动到中点时，的面积为__________．

Answer 1

【答案】20

【解析】

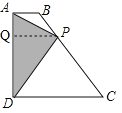
由函数图象上的点（6，32）、（10，0）的实际意义可知AB+BC、AB+BC+CD的长及△PAD的最大面积，从而求得AD、CD的长，再根据点P运动到点B时得，从而求得AB的长，最后根据梯形的中位线定理可求得当P运动到BC中点时，△PAD的面积．

解：由图象可知，AB+BC=12，AB+BC+CD=20，

∴CD=8，

根据题意可知，当P点运动到C点时，△PAD的面积最大，

， ∴AD=8，

又∵，

∴AB=2，

当P点运动到BC中点时，BP=PC，

如图，作PQ⊥AD于点Q，

∴AB∥PQ∥CD，

∴PQ为梯形ABCD的中位线，

则PQ= ，

∴△PAD的面积=

故答案为：20．