题目内容
【题目】如图,在△ABC中,分别以顶点A、B为圆心,大于![]() AB为半径作弧,两弧在直线AB两侧分别交于M、N两点,过M、N作直线MN,与AB交于点O,以O为圆心,OA为半径作圆,⊙O恰好经过点C.下列结论中,错误的是( )
AB为半径作弧,两弧在直线AB两侧分别交于M、N两点,过M、N作直线MN,与AB交于点O,以O为圆心,OA为半径作圆,⊙O恰好经过点C.下列结论中,错误的是( )
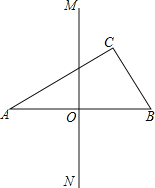
A.AB是⊙O的直径B.∠ACB=90°
C.△ABC是⊙O内接三角形D.O是△ABC的内心
【答案】D
【解析】
利用作法可判断点O为AB的中点,则可判断AB为⊙O的直径,根据圆周角定理得到∠ACB=90°,根据三角形内接圆的定义得到△ABC为⊙O的内接三角形,然后对选项进行判断.
解:由作法得MN垂直平分AB,则OA=OB,则AB为⊙O的直径,
∵⊙O恰好经过点C,
∴∠ACB=90°,△ABC为⊙O的内接三角形,点O为△ABC的外心.
故选:D.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目