题目内容
【题目】在等边![]() 中,点
中,点![]() 在边
在边![]() 上,以
上,以![]() 为半径的
为半径的![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.
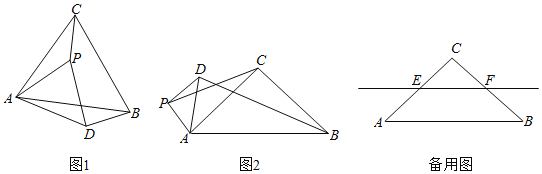
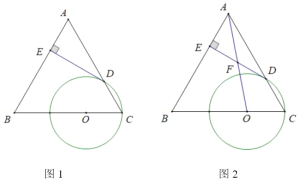
(1)如图1,求证:![]() 为
为![]() 的切线;
的切线;
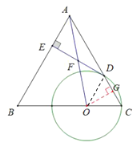
(2)如图2,连接![]() 交
交![]() 于点
于点![]() ,若
,若![]() 为
为![]() 中点,求
中点,求![]() 的值.
的值.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)连接![]() ,根据等边三角形的性质可得
,根据等边三角形的性质可得![]() ,然后根据等边对等角和平行线的判定可知
,然后根据等边对等角和平行线的判定可知![]() ,然后根据平行线的性质可证
,然后根据平行线的性质可证![]() ,最后根据切线的判定定理即可证出结论;
,最后根据切线的判定定理即可证出结论;
(2)过点![]() 作
作![]() 于
于![]() ,根据锐角三角函数求出
,根据锐角三角函数求出![]() ,然后利用AAS证出
,然后利用AAS证出![]() ,求出AG=5DG,利用锐角三角函数即可求出结论.
,求出AG=5DG,利用锐角三角函数即可求出结论.
(1)证明:连接![]() ,
,
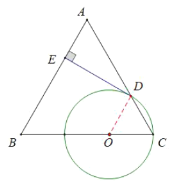
![]() 为等边三角形,
为等边三角形,
![]() ,
,
∵OC=OD
![]() ,
,
![]() ,△OCD为等边三角形
,△OCD为等边三角形
而![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() 为
为![]() 的切线.
的切线.
(2)解:过点![]() 作
作![]() 于
于![]() ,
,
∵OC=OD
∴CG=DG
在![]() 中,tanC=
中,tanC=![]()
∴![]() ,
,
由(1)知:![]() ,又有点
,又有点![]() 为
为![]() 中点,
中点,
∴AF=OF
在△FEA和△FDO中
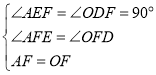
![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ·cos∠DAE=2AE,
·cos∠DAE=2AE,
![]() ,
,
∴AG=5DG
在![]() 中,
中,![]() ,
,
即![]() .
.

练习册系列答案
相关题目