题目内容
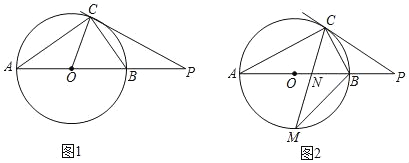
【题目】已知,AB是⊙O的直径,点C在⊙O上,点P是AB延长线上一点,连接CP.
(1)如图1,若∠PCB=∠A.
①求证:直线PC是⊙O的切线;
②若CP=CA,OA=2,求CP的长;
(2)如图2,若点M是弧AB的中点,CM交AB于点N,MNMC=9,求BM的值.
【答案】(1) ①见解析;②2![]() ;(2)3.
;(2)3.
【解析】
(1)①由等腰三角形的性质和圆周角定理可得OC⊥CP,即可得出结论;
②根据圆周角定理及三角形内角和定理得出∠P=30°,根据30°角所对直角边等于斜边的一半即可得出结论;
(2)根据圆周角定理可证△AMC∽△NMA,再根据相似三角形的对应边成比例即可得出结论.
(1)①∵OA=OC,∴∠A=∠ACO.
∵∠PCB=∠A,∴∠ACO=∠PCB.
∵AB是⊙O的直径,∴∠ACO+∠OCB=90°,∴∠PCB+∠OCB=90°,即OC⊥CP.
∵OC是⊙O的半径,∴PC是⊙O的切线.
②∵CP=CA,∴∠P=∠A,∴∠COB=2∠A=2∠P.
∵∠OCP=90°,∴∠P=30°.
∵OC=OA=2,∴OP=2OC=4,∴PC=![]() =
=![]() ;
;
(2)连接MA、MB.
∵点M是弧AB的中点,∴AM=BM,∴∠ACM=∠BAM.
∵∠AMC=∠AMN,∴△AMC∽△NMA,∴![]() ,∴AM2=MCMN.
,∴AM2=MCMN.
∵MCMN=9,∴AM=3,∴BM=AM=3.

【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),则当售价x定为多少元时,厂商每天能获得最大利润?最大利润是多少?
(3)如果超市要获得每天不低于1350元的利润,且符合超市自己的规定,那么该商品每千克售价的取值范围是多少?请说明理由.