题目内容
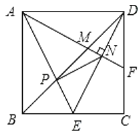
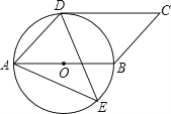
【题目】 如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45°.
(1)判断CD与⊙O的位置关系,并说明理由;
(2)若⊙O半径为4cm,AE=6cm,求∠ADE的正切值.
【答案】(1)CD与⊙O相切,理由见解析;(2)![]()
【解析】
(1)连接OD,首先根据圆周角定理求出∠AOD=90°,然后利用平行四边形的性质得到AB∥DC,利用平行线的性质即可得出结论;
(2)连接BE,则∠ADE=∠ABE,由AB是⊙O的直径得到∠AEB=90°,而AB=2×4=8(cm).在Rt△ABE中,根据勾股定理求出BE的长,再利用三角函数的定义即可求解.
解:(1)CD与⊙O相切.
理由如下:连接OD.
则∠AOD=2∠AED=2×45°=90°,
∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠CDO=∠AOD=90°.
∴OD⊥CD,
∴CD与⊙O相切;
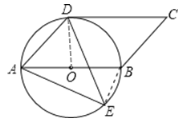
(2)连接BE,则∠ADE=∠ABE.
∵AB是⊙O的直径,
∴∠AEB=90°,AB=2×4=8(cm).
在Rt△ABE中,
由勾股定理得,BE=![]() (cm),
(cm),
∴tan∠ABE=![]() .
.
∴∠ADE的正切值为![]() .
.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案【题目】数学综合实践课上,老师提出问题:如图,有一张长为![]() ,宽为
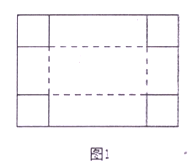
,宽为![]() 的长方形纸板,在纸板四个角剪去四个相同的小正方形,然后把四边折起来(实线为剪裁线,虚线为折叠线),做成一个无盖的长方体盒子,问小正方形的边长为多少时,盒子的体积最大?为了解决这个问题,小明同学根据学习函数的经验,进行了如下的探究:
的长方形纸板,在纸板四个角剪去四个相同的小正方形,然后把四边折起来(实线为剪裁线,虚线为折叠线),做成一个无盖的长方体盒子,问小正方形的边长为多少时,盒子的体积最大?为了解决这个问题,小明同学根据学习函数的经验,进行了如下的探究:
(1)设小正方形的边长为![]() ,长方体体积为
,长方体体积为![]() ,根据长方体的体积公式,可以得到
,根据长方体的体积公式,可以得到![]() 与
与![]() 的函数关系式是 ,其中自变量
的函数关系式是 ,其中自变量![]() 的取值范围是 ;
的取值范围是 ;
(2)列出![]() 与
与![]() 的几组对应值如下表:
的几组对应值如下表:
| … |
|
|
|
|
|
|
| 1 |
|
| … |
| … | 1.3 | 2.2 | 2.7 | 3.0 | 2.8 | 2.5 | 1.5 | 0.9 | … |
(注:补全表格,保留1位小数点)
(3)如图,请在平面直角坐标系中描出以补全后表格中各对对应值为坐标的点,画出该函数图象;
(4)结合函数图象回答:当小正方形的边长约为 ![]() 时,无盖长方体盒子的体积最大,最
时,无盖长方体盒子的体积最大,最
大值约为 .