题目内容
【题目】如图,四边形ABCD中,∠ABC=30°,∠ADC=60°,AD=DC.
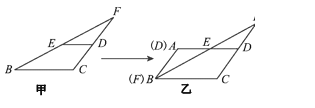
(操作)(1)将△ABD绕点D沿顺时针方向旋转60°,在图中画出旋转后的三角形.
(探究)(2)结合所画图形探究BD与AB,BC之间的数量关系,并证明你的结论.
(应用)(3)若AB=6,BC=8,试求四边形ABCD的面积.

【答案】(1)见解析;(2)BD2=AB2+BC2,见解析;(3)![]()
【解析】
(1)分别利用旋转的旋转画出A,B旋转后的对应点,而D为旋转中心与自身对应,然后顺次连接三对应点得到答案.
(2)连接BE,利用旋转的旋转证明△DBE是等边三角形,再证明![]() 为直角三角形,利用等量代换可以得到答案.
为直角三角形,利用等量代换可以得到答案.
(3)利用(2)的结论求BD,再求等边三角形DBE的面积,直角三角形BEC的面积,利用图形旋转前后面积不变,把四边形的面积转化为等边三角形DBE的面积减去直角三角形BEC的面积即可.
(1)如图,利用旋转性质作![]() ,然后在
,然后在![]() 角的边上截取
角的边上截取![]() ,得A的对应点C,B的对应点E,顺次连接D,C,E得到旋转后的
,得A的对应点C,B的对应点E,顺次连接D,C,E得到旋转后的![]() .
.
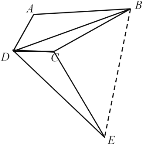
【探究】
(2)BD与AB,BC数量关系:BD2=AB2+BC2
理由:连接BE
由旋转可知
∠DCE=∠A,CE=AB
DE=DB,∠BDE=60°,
∴△DBE是等边三角形
∴BE=DB
∵∠ADC+∠ABC=60°+30°=90°
∴∠A +∠DCB=360°-90°=270°
∠DCE +∠DCB=270°
∴∠ECB=90°
∴BC2+CE2=BE2
∴BD2=AB2+BC2
【应用】
(3)因为BD2=AB2+BC2 AB=6,BC=8
所以BD=10,又△DBE是等边三角形
所以![]() ,
,
因为∠ECB=90°
所以△BCE的面积为24,
由旋转可知:
S四边形ABCD= S△DBE- S△BCE
=![]()

练习册系列答案
相关题目