题目内容
【题目】已知抛物线的顶点为(1，﹣4)，且过点(﹣2，5)．
（1）求抛物线的解析式；
（2）根据函数图象，直接写出y＜0时，自变量x的取值范围．
【答案】（1）y＝（x﹣1）2﹣4；（2）﹣1＜x＜3
【解析】
（1）直接利用顶点式求出二次函数解析式即可；
（2）首先求出图象与x轴交点，再利用抛物线图象得出当函数值y＜0时，自变量x的取值范围．
解：（1）设抛物线解析式为：y＝a（x﹣1）2﹣4，
把点（﹣2，5）代入得：
5＝a（﹣2﹣1）2﹣4，
解得：a＝1，
故抛物线解析式为：y＝（x﹣1）2﹣4；
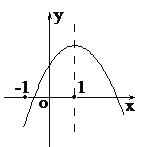
（2）当y＝0可得，0＝（x﹣1）2﹣4，
解得：x1＝3，x2＝﹣1，
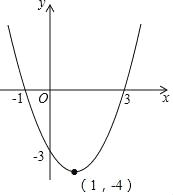
故抛物线与x轴的交点为：（﹣1，0），（3，0），
如图所示：
，
可得：当函数值y＜0时，自变量x的取值范围为：﹣1＜x＜3．
练习册系列答案
名校课堂系列答案
相关题目
