题目内容
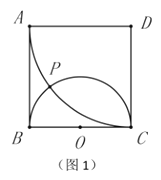
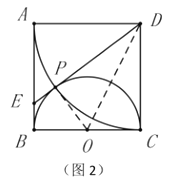
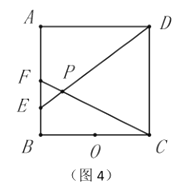
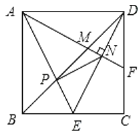
【题目】如图，正方形ABCD的边长为2，点E是BC的中点，AE与BD交于点P，F是CD上一点，连接AF分别交BD，DE于点M，N，且AF⊥DE，连接PN，则以下结论中：①F为CD的中点；②3AM=2DE；③tan∠EAF＝
；④
；⑤△PMN∽△DPE，正确的结论个数是（ ）
A.1个B.2个C.3个D.4个
【答案】D
【解析】
逐个结论进行判断：
①证明△ECD≌△FDA（AAS），即可得出结论F为CD的中点；
②根据△ABM和△FDM组成的沙漏模型，利用相似三角形对应线段成比例即可判断；
③在Rt△ANE中，tan∠EAF＝
，在△ADE和△ADF中分别运用面积法求出AN，DN，运用勾股定理求出DE，则EN=DE-EN，据此计算判断；
④作PH⊥AF于H，通过构造直角三角形，运用相似模型和勾股定理求出PN；
⑤由PN≠DN，推出对应角不相等，即可得出结论．
①F为CD的中点；
∵ABCD是正方形
∴AB=BC=AD=CD=2，∠FDA=∠ECD=90°
∵AF⊥DE
∴∠CDE+∠AFD=90°
又∵∠CDE+∠DEC=90°
∴∠AFD=∠DEC
∴△ECD≌△FDA（AAS）
∴DF=CE
∵E是BC的中点
∴F是CD的中点
故结论①正确；
②3AM=2DE；
∵AB∥DC
∴
∴
由①知：AF=DE
∴3AM=2DE
故结论②正确．
③tan∠EAF＝
；
由勾股定理得：
AF=DE=AE=
∵S△ADE=
×2×2=×
×AN
∴AN=
∵S△ADF=×2×1=××DN
∴DN=
∴EN=DE-DN=
=
∴tan∠EAF==
故结论③正确．
④
；
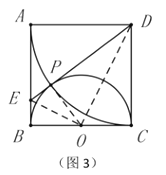
如图，作PH⊥AN于H
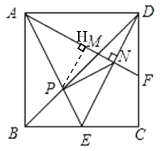
∵AD∥BE
∴
∴
∵FH∥EN
∴
∴AH=
，PH=
∴NH=
由勾股定理得：
故结论④正确．
⑤△PMN∽△DPE
∵PN≠DN
∴∠MPN≠∠PDE
∴△PMN与△DPE不相似
故结论⑤错误．
所以正确结论为①②③④．
故选：D
【题目】綦江区某中学的国旗护卫队需从甲、乙两队中选择一队身高比较整齐的队员担任护旗手，每队中每个队员的身高（单位：cm）如下:
甲队 | 178 | 177 | 179 | 179 | 178 | 178 | 177 | 178 | 177 | 179 |
乙队：
分析数据：两组样本数据的平均数、中位数、众数、方差如下表所示：
整理、描述数据:
平均数 | 中位数 | 众数 | 方差 | |
甲队 | 178 | 178 | b | 0.6 |
乙队 | 178 | a | 178 | c |
（1）表中a=______，b=______，c=______；
（2）根据表格中的数据，你认为选择哪个队比较好？请说明理由．
