题目内容
如下图,过四边形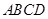 的四个顶点分别作对角线
的四个顶点分别作对角线 的平行线,所围成的四边形
的平行线,所围成的四边形 显然是平行四边形。在进一步学习时,小明和小亮产生了很大的意见分歧:
显然是平行四边形。在进一步学习时,小明和小亮产生了很大的意见分歧:
小明说:如果一个是平行四边形 是矩形,则四边形
是矩形,则四边形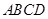 一定是菱形;
一定是菱形;
小亮说:如果一个平行四边形 是矩形,则四边形
是矩形,则四边形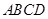 一定是对角线互相垂直的四边形,而不一定是矩形。
一定是对角线互相垂直的四边形,而不一定是矩形。
(1)你认为谁的观点是错误的。
(2)如果四边形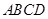 对角线相等,平行四边形
对角线相等,平行四边形 形状为
形状为
(3)如果四边形 为正方形,则四边形
为正方形,则四边形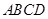 必须满足条件 ,
必须满足条件 ,
并且在下面的网格中画出符合条件(3)的图形并说明理由。
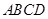 的四个顶点分别作对角线
的四个顶点分别作对角线 的平行线,所围成的四边形
的平行线,所围成的四边形 显然是平行四边形。在进一步学习时,小明和小亮产生了很大的意见分歧:
显然是平行四边形。在进一步学习时,小明和小亮产生了很大的意见分歧:小明说:如果一个是平行四边形
 是矩形,则四边形
是矩形,则四边形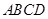 一定是菱形;
一定是菱形;小亮说:如果一个平行四边形
 是矩形,则四边形
是矩形,则四边形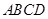 一定是对角线互相垂直的四边形,而不一定是矩形。
一定是对角线互相垂直的四边形,而不一定是矩形。(1)你认为谁的观点是错误的。
(2)如果四边形
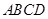 对角线相等,平行四边形
对角线相等,平行四边形 形状为
形状为 (3)如果四边形
 为正方形,则四边形
为正方形,则四边形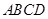 必须满足条件 ,
必须满足条件 ,并且在下面的网格中画出符合条件(3)的图形并说明理由。

(1)小明的观点是错误的。
(2)菱形
(3)四边形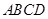 必须满足条件为对角线互相垂直且相等
必须满足条件为对角线互相垂直且相等
能画出符合条件的图
如网格中图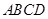 中AC⊥BD且AC=BD
中AC⊥BD且AC=BD
∵EF∥AC∥HG,HE∥DB∥GF,AC⊥BD
∴ACGH、DBFG、EFGH为平行四边形,
∠HAC=90º,∠AHG=90º
∴HG=AC,GF=BD,EFGH为矩形
∵AC=BD
∴HG=GF
∴EFGH为菱形

(2)菱形
(3)四边形
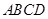 必须满足条件为对角线互相垂直且相等
必须满足条件为对角线互相垂直且相等 能画出符合条件的图
如网格中图
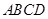 中AC⊥BD且AC=BD
中AC⊥BD且AC=BD∵EF∥AC∥HG,HE∥DB∥GF,AC⊥BD
∴ACGH、DBFG、EFGH为平行四边形,
∠HAC=90º,∠AHG=90º
∴HG=AC,GF=BD,EFGH为矩形
∵AC=BD
∴HG=GF
∴EFGH为菱形

(1)根据菱形和矩形的判定方法,可以直接判定小明和小亮的观点谁正确.
(2)根据菱形的判定方法可知,如果四边形ABCD对角线相等,那么平行四边形EFGH是菱形.
(3)根据正方形的性质,可知四边形ABCD必须满足条件为对角线互相垂直且相等,先判定ACGH、DBFG、EFGH为平行四边形,再证明EFGH为矩形且为菱形,即四边形EFGH为正方形.
(2)根据菱形的判定方法可知,如果四边形ABCD对角线相等,那么平行四边形EFGH是菱形.
(3)根据正方形的性质,可知四边形ABCD必须满足条件为对角线互相垂直且相等,先判定ACGH、DBFG、EFGH为平行四边形,再证明EFGH为矩形且为菱形,即四边形EFGH为正方形.

练习册系列答案
相关题目